隐马尔科夫模型 - Evan Hou的博客

隐马尔科夫模型是一个并不复杂的数学模型，到目前为止，他一直被认为是解决大多数的自然语言处理问题最为快速、有效的方法。它成功地解决了复杂的语音识别、机器翻译等问题。

1.马尔科夫链

马尔科夫过程是俄国数学家A.A.马尔科夫提出的，其原始模型为马尔科夫链。马尔科夫链是指时间和状态都是离散的马尔科夫过程。该过程具有如下特性：在已知系统当前状态的条件下，它未来的演变不依赖于过去的演变。也就是说，一个马尔科夫过程可以表示为系统在状态转移过程，第T+1次结果只受第T次结果的影响，即只与当前状态有关，而与过去状态，即系统的初始状态和此次转移前的所有状态无关。举一个大家熟悉的例子，我们可以把$s_1,s_2,s_3,···,s_t···$看成是北京每天的最高气温，这里面每个状态$s_t$都是随机的。第二，任一状态$s_t$的取值都可能和周围其他的状态相关。回到上面的例子，任何一天的最高气温，与这段时间以前的最高气温是相关的。这样随机过程就有了两个维度的不确定性。马尔科夫为了简化问题，提出了一种简化的假设，即随机过程中各个状态$s_t$的概率分布，只与它的前一个状态$s_{t-1}$有关，即$P(s_t \mid s_1,s_2,s_3···,s_{t-1} )=P(s_t \mid s_{t-1})$。比如，对于天气预报，硬性假设今天的气温只跟昨天有关而与前天无关。当然这种假设未必合适所有应用，但是至少对以前很多不好解决的问题给出了近似解。这个假设后来被命名为马尔科夫假设，而符合这个假设的随机过程则称为马尔科夫过程，也称为马尔科夫链。

2.隐马尔科夫模型

图1所示为隐马尔科夫模型。一个隐马尔科夫模型(HMM)由两组状态集合和三组概率集合构成。

隐状态：系统的(真实)状态序列，可以由一个马尔科夫过程进行描述。
状态转移矩阵：是隐状态空间，即马尔科夫状态空间的状态转移矩阵。
观察状态：在这个过程中显示状态序列。
Π向量：从一个观察状态到每个隐状态的概率向量(初始概率)，表示为初始时刻观察状态转换到隐状态的概率。
混淆矩阵：也称为发射概率，包含了每个给定的观察状态转换到每个隐藏状态的概率矩阵。

HMM

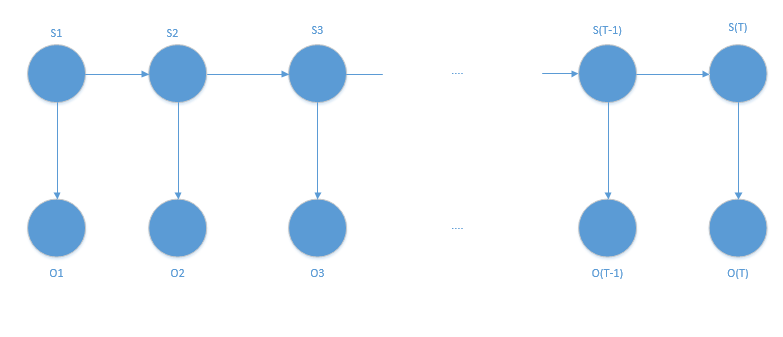
根据上述描述，可以给出隐马尔科夫模型如下的形式化定义。

一个隐马尔科夫模型是一个五元组($S,O,\pi,A,B$)。

S：一个系统在t时刻的状态(隐状态)空间几何($S_1，S_2···S_n$)
O：一个输出(观测状态)状态的集合($O_1,O_2,O_3···O_m$)
$Π=(Π_i$)：初始化概率向量。
A=($a_{ij}$)：状态转移矩阵。
B=($b_{ij}$)：混淆矩阵。

注意，这里t可以不表示事件，在状态转移矩阵及混淆矩阵中的每个概率都可以与时间无关，也就是说，当系统演化时这些矩阵并不一定随时间改变。

HMM中有三个基本问题

估计问题：给定一个观察序列$O=O_1O_2···O_T$和模型$μ=(A,B,Π)$，如何快速的计算出给定模型μ情况下，观察序列O的概率，即$P(O\mid μ)$？
序列问题：给定一个观察序列$O=O_1O_2···O_T$和模型$μ=(A,B,Π)$，如何快速有效的选择在一定意义下“最优”的状态序列$Q=q_1q_2···q_T$,使得该状态序列“最好地解释”观察序列？
训练问题或参数估计问题：给定一个观察序列$O=O_1O_2···O_T$，如何根据最大似然估计来求模型的参数值？即如何调节模型$μ=(A,B,Π)$的参数，使得$P(O \mid μ)$最大？

接下来，举例求解这个模型。因为比较容易懂，很多文献中都用到有关天气的例子。例如，假设我们的一个好朋友在国外，通过电话聊天，我们可以了解朋友所在城市的生活状态，比如晴天的时候，朋友会出去跑步，阴天的时候会窝在家里睡觉，下雨天的时候会喜欢看书，或者听音乐。这样我们可以从朋友的状态推测出朋友所在城市的天气情况。假设我们还知道一年中晴天，阴天和雨天的总比例，也就是初始向量，还知道每种天气间的转移概率，以及朋友做每件事对应天气的发射概率。具体模型如图2所示。

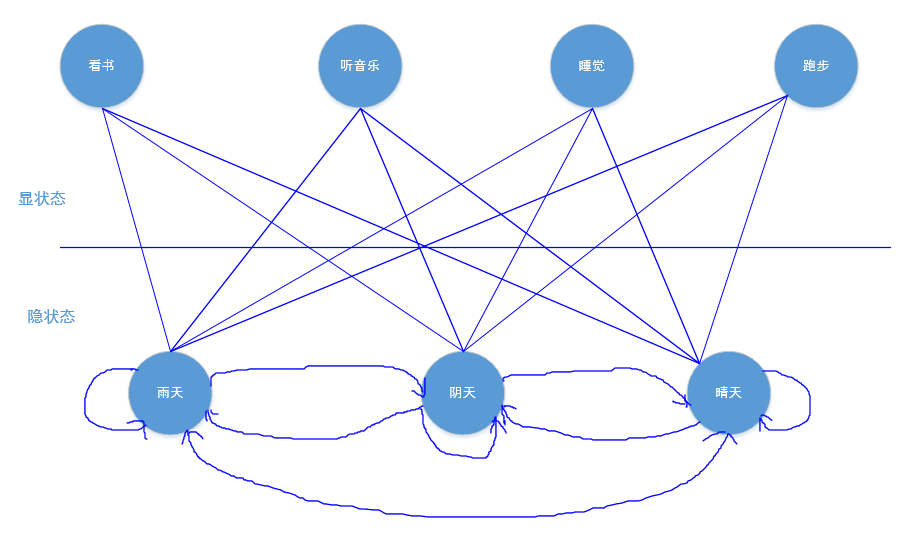
forest

由图2可知：

S是天气系统在t时刻的状态空间集合：{晴天，阴天，雨天}。
O是一个输出状态的集合：{看书，听音乐，睡觉，跑步}。
初始化概率向量Π：{0.63,0.17,0.20}，表示一年中晴天、阴天、雨天的概率。
状态转移矩阵A(见表1)。

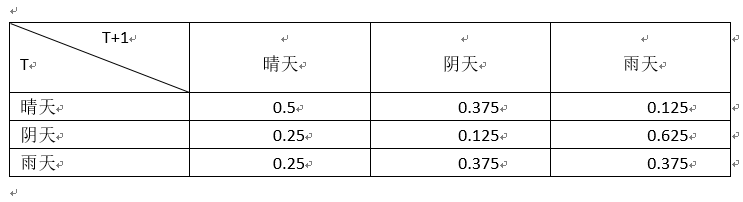
混淆矩阵B(发射概率)，如表2所示。

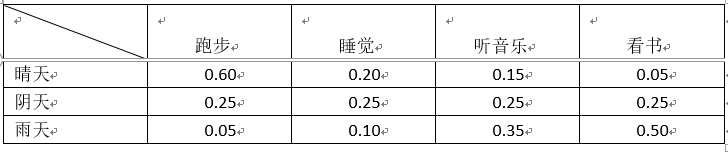
chart2

假设朋友连续三天的显状态为(跑步，睡觉，看书)，然后你想预测这三天的天气状态：隐状态序列。

那么很自然，天气预测就转换为如图3所示的形式。

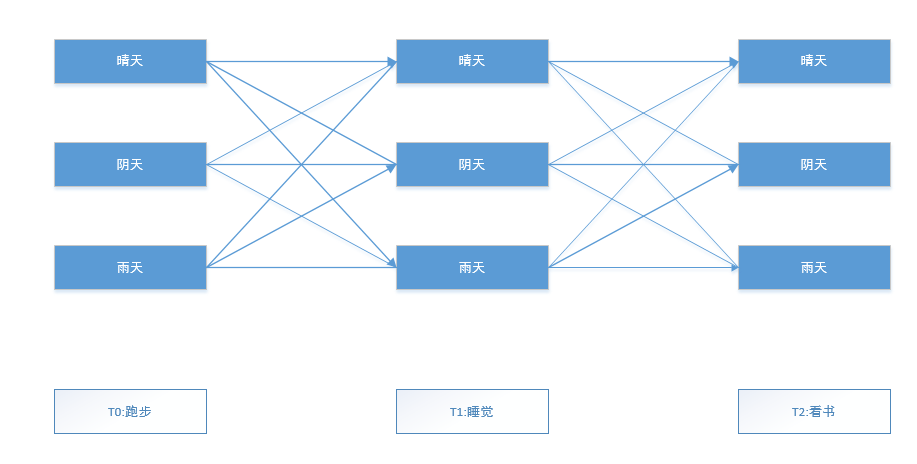
根据马尔科夫链的规则，预测这三天的天气状况，实际上就是计算$T_0$~$T_2$三天中所有路径中最大的一条，但现在多了一个显状态，以及该显状态对应隐状态的发射概率。前向算法的求解过程如下。

给出这三天的显状态序列：(跑步，睡觉，看书)。为了泛化计算，也给出一般化的形式：($b_{k1},b_{k2}···b_{kr}$)。

首先计算最初的状态。这一步最简单，初始状态为Π。初始$t_0$的显状态为跑步，则

$a_1(晴天)=0.63×0.6=0.378$
$a_1(阴天)=0.17×0.25=0.0425$
$a_1(雨天)=0.20×0.05=0.01$

其中，$b_{jkl}$是混淆矩阵，也称发射概率，j代表天气状态序列，k表示朋友的生活状态(观察序列)；Π为初始化概率向量，其初始值为(0.63,0.17,0.20)，得到的$a_1(j)$是第一天的转移概率。

然后计算最大概率的那个天气状态:$argmax(α(j))$。很显然最大概率的天气状态为$α_1(晴天)$，最大的概率为0.378.

接下来计算第二题的状态转移概率，因为后一天状态由前一天来决定(马尔科夫性)，同时第二天的转移概率也受第二天的显状态影响。与第一天相似，使用已经得到的$a_1(j)$，以及显状态睡觉的发生概率，$a_2(j)$的计算过程如下。

$a_2(晴天)=(0.378×0.5+0.0425×0.25+0.01×0.25)×0.2=0.04025$
$a_2(阴天)=(0.378×0.375+0.0425×0.125+0.01×0.0375)×0.25=0.037703125$
$a_2(雨天)=(0.378×0.125+0.0425×0.625+0.01×0.0375)×0.1=0.00775625$

形式化上述的运算如下：$α_{t+1}(j)=b_{jkt+1}\sum_{i=1}^n α_t(j)α_{ij}$

其中，$b_{jkt+1}$是t+1时刻的混淆矩阵，也称为发射概率，j代表天气状态序列，k代表朋友的生活状态(观察状态)序列；得到的$a_t(j)$是当时时间的状态转移概率，那么t+1指的是下一时刻，$a_{ij}$是隐状态的转移概率。

同样，计算最大概率的那个天气状态：$argmax(α_{t+1}(j))$.同样，最大概率的天气状态为$a_2(晴天)$，最大的概率为0.04025。

最后，计算第三题的状态转移概率。同样，最后一天的状态由前一天来决定，同时最后一天的转移概率也受前一天的显状态影响。与第二天的计算公式相同，使用已经得到的$a_2(j)$，以及显状态看书的发生概率，$a_3(j)$的计算过程如下：

$a_3(晴天)=(0.040425×0.5+0.037703125×0.25+0.00775625×0.25)×0.05=0.0015788671875$
$a_3(阴天)=(0.040425×0.375+0.037703125×0.125+0.00775625×0.375)×0.25=0.00569521484375$
$a_3(雨天)=(0.040425×0.125+0.037703125×0.625+0.00775625×0.375)×0.5=0.0157630859375$

运算公式与(3)相同：$α_{t+1}(j)=b_{jkt+1}\sum_{i=1}^n α_t(j)α_{ij}$和$argmax(α_{t+1}(j))$。同样，最大概率的天气状态为$s_3(雨天)$，最大概率为0.0157630859375。

根据输出概率得到每天的最大概率值。得到最终的推理结果为晴天→晴天→雨天。

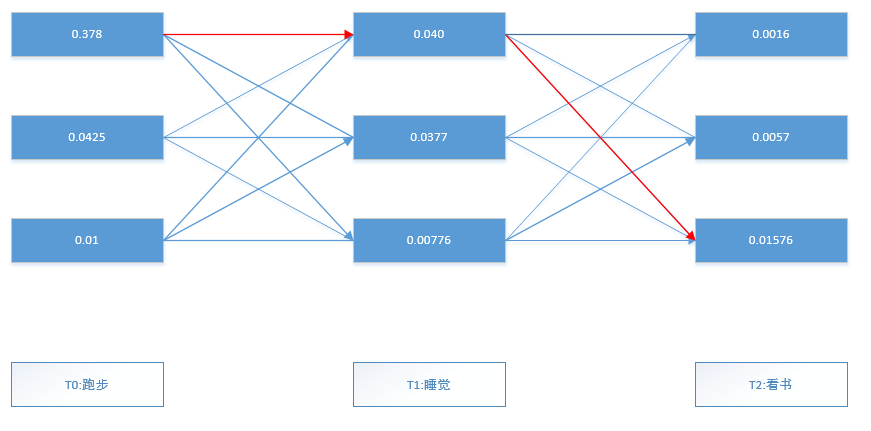
python算法代码如下：

   #-*- coding:utf-8  -*- 
from numpy import *
   startP=mat([0.63,0.17,0.20]) #起始概率
stateP=mat([[0.5,0.25,0.25],[0.375,0.125,0.375],[0.125,0.675,0.375]])
   #状态转移概率
   emitP=mat([[0.6,0.20,0.05],[0.25,0.25,0.25],[0.05,0.10,0.501]])#发射(混合)概率
   
   state1Emit=multiply(startP,emitP[:,0].T)
   print (state1Emit)
   print ("argmax:",state1Emit.argmax())
   
#计算干燥的概率
   state2Emit=stateP*state1Emit.T
   state2Emit=multiply(state2Emit,emitP[:,1])
   print(state2Emit)
print("argmax:",state2Emit.argmax())
   #计算潮湿的概率
   state3Emit=stateP*state2Emit
   state3Emit=multiply(state3Emit,emitP[:,2])
   print(state2Emit)
   print("argmax:",state3Emit.argmax())

结果输出如下：

   [[ 0.378   0.0425  0.01  ]]
argmax: 0
   [[ 0.040425  ]
 [ 0.03770312]
    [ 0.00796875]]
   argmax: 0
   [[ 0.040425  ]
    [ 0.03770312]
    [ 0.00796875]]
   argmax: 2

显然，随着矩阵的规模增大，算法的计算量是灾难性的。下面思考简化计算过程。

4.Viterbi算法的实现

维特比算法用于求解HMM中第二个问题，给定一个观察序列$O=O_1O_2···O_T$和模型$μ=(A,B,Π)$，如何快速有效的选择在一定意义下“最优”的状态序列$Q=q_1q_2···q_T$,使得该状态序列“最好地解释”观察序列？这个问题的答案并不是唯一的，因为它取决于对“最优状态序列”的理解。一种理解是，是该状态序列中每一个状态都单独的具有最大概率，即要使得 $γ_t(i)=P(q_t=s_i\mid O,μ)最大$

根据这种对“最优状态序列”的理解，如果只考虑每个状态的出现都单独的达到最大概率，而忽略了状态序列中两个状态之间的关系，很可能导致两个状态$q_t$和$q_{t+1}$之间的转移概率为0.即$q_tq_{t+1}=0$。那么，在这种情况下，所谓的“最优状态序列”根本就不是合法的序列。因此，我们常常采用另一种对“最优状态序列”的理解：在给定模型μ和观察序列O的条件下，使条件概率$P(Q \mid O,μ)$最大的状态序列，即 $Q=argmaxP(Q \mid O,μ)$ 这种理解避免了前一种理解所引起的“断序”的问题。根据这种理解，优化的不是状态序列中的单个序列，而是整个状态序列，不合法的状态序列的概率为0，因此，不可能被选为最优状态序列。

维特比算法运用动态规划的搜索算法求解这种最优状态序列。为了实现这种搜索，首先定义一个维特比变量$δ_t(i)$.

维特比变量$δ_t(i)$是在时间t时，HMM沿着某一条路经到达状态$s_i$，并输出观察序列$O=O_1O_2···O_t$的最大概率。

为了记录在t时间时，HMM通过哪一条概率最大的路径到达状态$s_i$，维特比算法设置了另外一个变量$ψ_t(i)$用于路径记忆，让$ψ_t(i)$记录该路径上状态$s_i$的前一个(在时间t-1)状态。

最初状态的计算与前面相同。

$a_1(晴天)=0.63×0.6=0.378$
$a_1(阴天)=0.17×0.25=0.0425$
$a_1(雨天)=0.20×0.05=0.01$

然后计算最大概率的那个天气状态：$arg max(δ(i,t))$.

计算结果为δ(晴天，1)概率为0.378.

接下来计算第二天的状态转移概率：$δ_t(i)=max(δ_{t-1}(j)α_{ji}b_{ikt})$。

$a_2(晴天)=max(0.378×0.5,0.0425×0.25,0.01×0.25)×0.2=0.0378$
$a_2(阴天)=max(0.378×0.375,0.0425×0.125,0.01×0.0375)×0.25=0.0354375$
$a_2(雨天)=max(0.378×0.125,0.0425×0.625,0.01×0.0375)×0.1=0.004725$

同样，计算最大概率的那个天气状态：$arg max(δ(i,t))$.

计算结果为δ(晴天，2)概率为0.0378.

最后计算第三天的状态转移概率。

$a_3(晴天)=max(0.0378×0.5,0.0354375×0.25,0.004725×0.25)×0.05=0.00945$
$a_3(阴天)=max(0.0378×0.375,0.0354375×0.125,0.00472×0.375)×0.25=0.00354375$
$a_3(雨天)=max(0.0378×0.125,0.0354375×0.625,0.00472×0.375)×0.5=0.01107421875$

最后，计算最大概率的那个天气状态：$arg max(δ(i,t))$，δ(晴天，3)概率为0.01107421875.

根据最后一天的最大概率δ(晴天，3)概率为0.01107421875，我们逆向推出到达该状态最大概率的路径：晴天→阴天→雨天。