Logistic 回归(Logistic Regression,LR)是一种常用的处理分类问题的线性模型。逻辑回归模型仅在线性回归的基础上,套用了一个逻辑函数, 但也就由于这个逻辑函数,使得逻辑回归模型成为了机器学习领域一颗耀眼的明星。
逻辑回归模型
回归是一种极易理解的模型,假设现在有一些数据点,我们用一条直线对这些点进行拟合(该线称为最佳拟合直线),这个拟合过程就称作回归。利用Logistic回归进行分类的主要思想是:根据现有的数据对分类边界线建立回归公式,以此进行分类。这里的“回归”一词源于最佳拟合,表示找到最佳拟合参数集。训练分类器时的做法就是寻找最佳拟合参数,使用的是最优化算法。
举个例子,回归就相当于$y=f(x)$,表明自变量x与因变量y的关系。最常见问题如医生治病时的望、闻、问、切,之后判定病人是否生病了或者生了什么病,其中的望闻问切就是获取自变量x,即特征数据,判断是否生病就相当于获取因变量y,即预测分类。
最简单的回归是线性回归,在此借用吴恩达的讲义,线性回归假设特征和结果满足线性关系。其实线性关系的表达能力非常强大,每个特征对结果的影响强弱可以由前面的参数体现,而且每个特征变量可以首先映射到一个函数,然后再参与线性计算。这样就可以表达特征与结果之间的非线性关系。我们用$X_1,X_2,···X_n$去描述feature里面的分量,比如$x1=是否吸烟$,$x2=作息规律$,等等,我们可以做出一个估计函数:
\[h(x)=h_θ(x)=θ_0+θ_1x_1+θ_2x_2\]θ在这儿称为参数,在这的意思是调整feature中每个分量的影响力,就是到底是吸烟还是作息规律对患脑瘤的影响更大。
如下图所示,X为数据点——肿瘤大小,Y为观测值——是否是恶性肿瘤。通过构建线性回归模型,如$h_Θ(x)$所示,构建模型后,既可以根据肿瘤大小,预测是否为恶性肿瘤$h_Θ(x)≥0.5$为恶性,$h_Θ(x)<0.5$为良性。
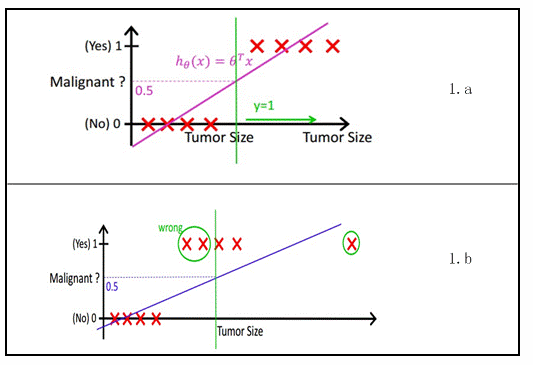
然而线性回归的健壮性很差,例如在上图b中的数据上建立回归,因最右边噪点的存在,使回归模型在训练集上表现都很差。这主要是由于线性回归在整个实数域内敏感度一致,而分类范围,需要在[0,1]。逻辑回归就是一种减小预测范围,将预测值限定在[0,1]间的一种回归模型,其回归方程与回归曲线下图所示。逻辑曲线在z=0时,十分敏感,在$z>>0$或$z«0$处,都不敏感,将预测值限定为(0,1)。逻辑回归其实仅为在线性回归的基础上,套用了一个逻辑函数。我们想要的函数应该是,能接受所有的输入然后预测出类别。所以,逻辑回归引入logistic函数,将分类器输出界定在$[0,1]$之间,其一般形式可表示为为$f_\theta(x)=g(\theta^Tx)$。那么问题来了,我们到底需要选择什么样形式的logistic函数$g(z)$?
需要强调的是,我们不选用线性回归的原因是线性回归不能保证预测值的范围位于$[0,1]$之间。所以,针对该问题最简单的方法是移除因变量值域的限制,这样,我们就要对概率形式做某种变化。
然后,在众多非线性函数中,log函数的值域为整个实数域且单调,因此,我们可以计算优势比的对数,令$\eta=log(odds)=log\frac{p}{1-p}=logit(p)$。
经过以上两步,我们可以去除分类问题对因变量值域的限制,如果概率等于0,那么优势比则为0,logit值为$-\infty$;相反,如果概率等于1,优势比为$\infty$,logit的值为$\infty$。因此,logit函数可以将范围为$[0,1]$的概率值映射到整个实域空间,当概率值小于0.5时,logit值为负数,反之,logit值为正数。
综上所述,我们解决了分类问题对分类器预测的因变量值域的限制,我们就可以采用线性回归对一一映射后的概率值进行线性拟合,即
\[logit(p)=log(\frac{p}{1-p})=\eta=f_{\theta}(x)=\theta^T*x\]因为logit变换是一一映射,所以存在logit的反变换(antilogit),我们可以求得$p$值的解析表达式:
\[p=antilogit(x)=logit^{\eta}=\frac{e^\eta}{1+e^\eta}=\frac{e^{\theta^T x}}{1+e^{\theta^Tx}}\] \[1-p=1-antilogit(x)=1-logit^{\eta}=1-\frac{e^\eta}{1+e^\eta=}=1-\frac{e^{\theta^Tx}}{1+e^{\theta^Tx}}=\frac{1}{1+e^{\theta^Tx}}\]众所周知,上式即为logitstic回归的一般表达式,其采用的logit变换一般记为sigmoid函数:
\[g(x)=\frac{e^{\theta^Tx}}{1+e^{\theta^Tx}}\]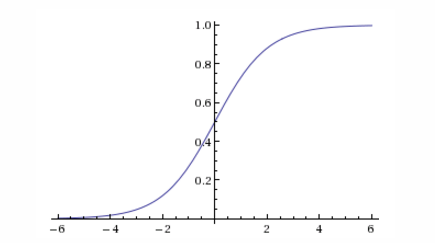
上图给出了Sigmoid函数在坐标系下的曲线图。当x为0时,Sigmoid函数为0.5.随着x的增大,对应的Sigmoid值将逼近与1;而随着x的减小,Sigmoid值将逼近于0.
因此,为了实现Logistic回归分类器,我们可以在每个特征上都乘以一个回归系数,然后把所有的结果值都相加,将这个总和代入Sigmoid函数中,进而得到一个在范围0~1之间的数值。任何大于0.5的数据被分入1类,小于0.5即被归入0类。所以Logistic回归也可以被看成一种概率估计。
确定了分类器的函数形式之后,现在的问题变成了:最佳回归系数是多少?如何确定他们的大小?这个问题将在下一节解答。
训练参数
Sigmoid函数的输入记为z,由下面公式得出:
\(z=w_0x_0+w_1x_1+···+w_nx_n\)
如果采用向量的写法,上述公式可以写成$z=w^Tx$,它表示将这两个数值向量对应元素相乘然后全部加起来即得到z值。其中的向量x是分类器的输入数据,向量w也就是我们要找到的最佳参数(系数),从而使得分类器尽可能地精确。为了寻找该最佳参数,需要用到最优化理论的一些知识。下面首先介绍梯度上升这一最优化方法,我们将学习到如何使用该方法求得数据集的最佳参数。最后我们将学习随机梯度上升算法,以及如何对其修改以获得更好的结果。
梯度上升法
这里介绍的第一个最优化算法叫做梯度上升法。梯度上升法基于的思想是:要找到某函数的最大值,最好的方法是沿着该函数的梯度方向探寻。如果梯度记为▽,则函数f(x,y)的梯度由下式表示:
\(▽f(x,y)=〔\frac{δf(x,y)}{δx} \frac{δf(x,y)}{δy} 〕\)
这是机器学习中最易造成混淆的一个地方,但在数学上并不难,需要做的只是牢记这些符号的意义。这个梯度意味着要沿x的方向移动$\frac{δf(x,y)}{δx} $,沿y的方向移动$\frac{δf(x,y)}{δy}$。其中,函数f(x,y)必须要在待计算的点上有定义并且可微。一个具体的函数例子如图-3所示。
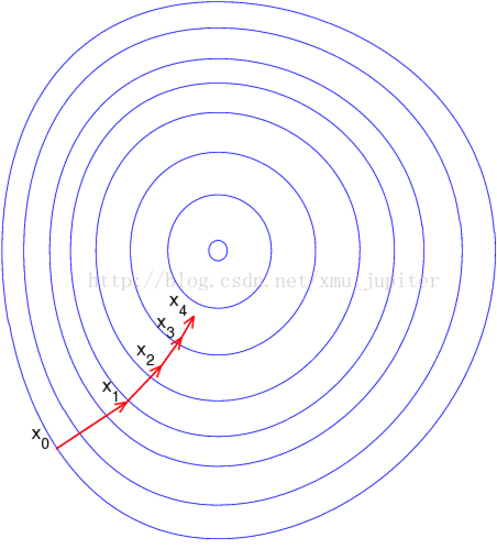
梯度上升算法到达每个点后都会重新估计移动方向。从$x_0$开始,计算完该点的梯度,函数就根据梯度移动到下一点$x_1$。在$x_1$点,梯度再次被重新计算,并沿着新的梯度方向移动到$x_2$。如此循环迭代,直到满足停止条件。迭代的过程中,梯度算子总是保证我们能选取到最佳的移动方向。
图-3中的梯度上升算法沿梯度方向移动了一步。可以看到梯度算子总是指向函数值增长最快的方向。这里说的是移动方向,而未提到移动量的大小。该量值称为步长,记做α。用向量来表示的话,梯度上升算法的迭代公式如下:
\(w:=w+α▽_wf(w)\)
该公式将一直被迭代执行,直至达到某个停止条件为止,比如迭代次数达到某个指定值或者算法达到某个可以允许的误差范围。
梯度下降和delta法则
我们经常听到的应该是梯度下降算法,它与这里的梯度上升算法一样,只是公式中加法需要变成减法。因此,对应的公式可以写成
\(w:=w_0-α▽_wf(w)\)
梯度上升算法用来求函数的最大值,而梯度下降算法用来求函数的最小值。
在感知器法则中,当训练样例线性可分时,感知器法则可以成功的找到一个权向量,但如果样例不是线性可分时它将不能收敛。因此,人们设计了另一个训练法则来克服这个不足,称为delta法则。如果训练样例不是线性可分的,那么delta法则会收敛到目标概念的最佳近似。
delta法则的关键思想是使用梯度下降来搜索可能的权向量的假设空间,以找到最佳拟合训练样例的权向量。这个法则很重要,因为它为反向传播算法提供了基础,而反向传播算法能够学习多个单元的互连网络。这个法则重要性的另一个原因是,对于包含多种不同类型的连续参数化假设的假设空间,梯度下降是必须遍历这样的假设空间的所以学习算法的基础。
最好把delta训练法则理解为训练一个无阈值的感知器,也就是一个线性单元。它的输出$o$如下:
\(o(\overrightarrow{x})=\overrightarrow{w}*\overrightarrow{x} \quad(1)\)
于是,线性单元对应于感知器的第一阶段,不带阈值。
为了推导线性单元的权值学习法则,先指定一个度量标准来衡量假设(权向量)相对于训练样例的训练误差。尽管有很多方法定义这个误差,一个常用的特别方便的度量标准为:
\[E(\overrightarrow{w})=\frac{1}{2} \sum_{d∈D}(t_d-o_d)^2 \quad(2)\]其中,D是训练样例的集合,$t_d$是训练样例的d的目标输出,$o_d$是线性单元对训练样例d的输出。在这个定义中,$E (\overrightarrow w)$是目标输出$t_d$和线性单元输出$o_d$的差异的平方在所有的训练样例上求和后的一半。这里我们把E定义为$\overrightarrow w$的函数,是因为线性单元的输出o依赖于这个权向量。
梯度下降法则的推导
为了确定一个使E最小化的权向量,梯度下降搜索从一个任意的初始权向量开始,然后以很小的步伐反复修改这个变量。每一步都是沿误差曲面产生最陡峭下降的方向修改向量,继续这个过程直到得到全局的最小误差点。
我们怎样才能计算出沿误差曲面最陡峭下降的方向呢?可以通过计算E相对向量$\overrightarrow w$的每个分量的倒数来得到这个方向。这个向量导数被称为E对于$\overrightarrow w$的梯度,记作$\bigtriangledown E(\overrightarrow w)$.
\[\bigtriangledown E(\overrightarrow w)=\lgroup \frac{δE}{δw_0},\frac{δE}{δw_1},···\frac{δE}{δw_n}\rgroup \quad(3)\]注意$\bigtriangledown E(\overrightarrow w)$本身是一个向量,它的成员是E对每个$w_i$的偏导数。当梯度被解释为全空间的一个向量时,它确定了使E最陡峭上升的方向。所以这个向量的反方向给出了最陡峭下降的方向。
既然梯度确定了E最陡峭上升的方向,那么梯度下降的训练法则是:
\[\overrightarrow w←\overrightarrow w+Δ \overrightarrow w\]其中:
\[Δ\overrightarrow w=-\eta \bigtriangledown E(\overrightarrow w) \quad(4)\]这里的$\eta$是一个正的常数叫做学习速率,它决定梯度下降搜索的步长。公式中的负号是因为我们想让权向量向E下降的方向移动。这个训练法则也可以写成它的 分量形式:
\[w_i←w_i+Δw_i\]其中:
\[Δw_i=- \eta \frac {δE}{δw_i} \quad(5)\]这样很清楚,最陡峭的下降可以按照比例$\frac{δE}{δw_i}$改变$\overrightarrow w$中的每一个$w_i$来实现。
要形成一个根据公式(5)迭代更新权的使用算法,我们需要一个高效的方法在每一步都计算这个梯度。幸运的是计算过程并不困难。我们可以从式(2)中计算E的微分,从而得到组成这个梯度向量的分量$\frac{δE}{δw_i}$。过程如下:
\[\begin{align} \frac{δE}{δw_i}=&\frac{δ\frac{1}{2}\sum_{d_\in D}(t_d-o_d)^2}{δw_i}=\frac{1}{2} \sum _{d \in D}\frac{δ(t_d-o_d)^2}{δw_i}\\&=\frac{1}{2}\sum_{d \in D}2(t_d-o_d)\frac{δ(t_d-o_d)}{δw_i} \\ &=\sum_{d \in D}(t_d-o_d)\frac{δ(t_d-\overrightarrow w*\overrightarrow x_d)}{δw_i} \end{align}\\\frac{δE}{δw_i}=\sum_{d \in D}(t_d-o_d)(-x_{id}) \quad (6)\]其中,$x_{id}$表示训练样例d的一个输入 分量$x_i$。现在我们有了一个公式,能够用线性单元的输入$x_{id}$、输出$o_d$以及训练样例的目标值$t_d$表示$\frac{δE}{δw_i}$。把公式(6)代入到公式(5)便得到了梯度下降权值更新法则。
\[Δ w_i=\eta \sum_{d \in D}(o_d-t_d)x_{id}\quad(7)\]总而言之,训练线性单元的梯度下降算法如下:选取一个初始的随机权向量;应用线性单元到所有的训练样例,然后根据公式(7)计算每个权值$Δw_i$;通过加上$Δw_i$来更新每个权值,然后重复这个过程。在整个样本集上的更新参数如下所示:
\[w_{t+1}\leftarrow w_t+\alpha\frac{1}{N}\sum^N_{n=1}x^{(n)}(y^{n}-\hat y^{(n)}_{w_t})\]其中$\alpha$是学习速率,$\hat y^{(n)}_{w_t}$是当参数为$w_t$时,logistic回归模型的输出。
训练算法
梯度上升法的伪代码如下:
每个回归系数初始化为1
重复R次
计算整个数据集的梯度
使用alpha×gradient更新回归系数的向量
返回回归系数
下面的代码是梯度上升算法的具体实现。
from numpy import *
'''
主要功能打开文件test.txt并逐行读取。
每行前两个值分别是X1和X2,第三个值是数据对应的类别标签
'''
def loadDataSet():
dataMat=[];
labelMat=[]
fr=open('testSet.txt')
for line in fr.readlines():
lineArr=line.strip().split()
dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
def sigmod(inX):
return 1.0/(1+exp(-inX))
def gradAscent(dataMatIn,classLabels):
#转换为Numpy矩阵数据类型
dataMatrix=mat(dataMatIn)
labelMat=mat(classLabels).transpose()
m,n=shape(dataMatrix)
print(m,n)
alpha=0.001 #alpha是向目标移动的步长
maxCycles=500 #迭代次数
#生成n*1的1矩阵
weights=ones((n,1))
#矩阵相乘
for k in range(maxCycles):
h=sigmod(dataMatrix*weights)
error=(labelMat-h)
weights=weights+alpha*dataMatrix.transpose()*error
return weights
随机梯度上升
梯度上升算法在每次更新回归系数时都要遍历整个数据集,该方法在处理100个左右的数据集尚可,但如果有数十亿样本和成千上万的特征,那么该方法的计算复杂度就太高了。一种改进方法是一次仅用一个样本点来更新回归系数,该方法称为“随机梯度上升算法”。由于可以在新样本到来时对分类器进行增量式更新,因而随机梯度上升算法是一个在线学习算法。与“在线学习”相对应,一次处理所有数据被称作为“批处理”。
随机梯度上升算法可以写成如下的伪代码:
所有回归系数初始化为1
对数据集中每个样本
计算该样本的梯度
使用alpha×gradient更新回归系数值
返回回归系数值
以下是随机梯度上升算法的实现代码。
随机梯度上升
def stocGradAscent0(dataMatrix,classLabels):
m,n=shape(dataMatrix)
alpha=0.01
weights=ones(n)
for i in range(m):
h=sigmod(sum(dataMatrix[i]*weights))
error=classLabels[i]-h
weights=weights+alpha*error*dataMatrix[i]
return weights
softmax回归
softmax 回归,也称多项或多类的logistic回归,是logistic回归在多类问题上的推广。
对于多类问题,类别表签$y \in {1,2,…,C}$可以有C个取值。给定一个样本$x$,softmax回归预测的属于类别$c$的条件概率为:
\[\begin{align} p(y=c\mid x )&=softmax(W^T_cX)\\ &=\frac{exp(W^T_cx)}{\sum^C_{c=1}(W^T_cX)} \end{align}\]其中$w_c$是第$c$类的权重向量。
softmax回归的决策函数可以表示为:
\[\begin{align} \hat y&=argmax^C_{c=1}P(y=c\mid x)\\ &=argmax^C_{c=1}W^T_cx \end{align}\]与logistic回归的关系,当类别数为2,softmax回归的决策函数为
\[\begin{align} \hat y&=argmax_{y\in \{0,1\}}W^T_yx\\ &=I(W^T_1X-W^T_0X>0)\\ &=I((W_1-W_0)^T X>0) \end{align}\]其中$I(.)$是指示函数。
小结
Logistic回归的目的是寻找一个非线性函数Sigmoid的最佳拟合参数,求解过程可以由最优化算法来完成。在最优化算法中,最常用的就是梯度上升算法,而梯度上升算法又可以简化为随机梯度上升算法。
随机梯度上升算法与梯度上升算法的效果相当,但占用更少的计算资源。此外,随机梯度上升是一个在线算法,它可以在新数据到来时完成参数更新,而不需要重新读取整个数据集来进行批处理运算。
参考
逻辑回归模型(Logistic Regression, LR)基础