随机场
随机场是一个随机推广过程的推广,使得底层的参数不再是一个简单的实数或整型“时间”,而是多维向量或点。在离散的情况下,随机场可以被认为是一组被确定在某个空间(如n维欧几里得空间)的离散点(随机数)列表。在统计学中,随机场可以看成一组随机变量的集合,而这组随机变量对应同一个样本空间。当然,这些随机变量之间常有某种依赖关系,一般来说,也只有当这些变量之间有依赖关系的时候,我们将其单独拿出来看成一个随机场才有实际意义。
因此,确定一个随机场有如下重要的要素。第一,随机过程包含了哪些不同的样本空间;第二,样本空间中的随机变量相互之间形成何种依赖关系(换个角度讲,就是条件独立的关系)。这两个因素是构成“随机场”的基本要件。
随机场包含如下两个要素:样本空间集合和单个样本空间中的随机变量集合。
我么不妨拿种地来打个比方。“不同分布的样本空间”好比一亩亩农田;“相互依赖的随机变量”好比种的各种庄稼,这就好比给随机场的每个“样本空间”里赋予不同取值范围的随机变量。通俗一点地讲,随机场就是在哪块地里种什么庄稼的事情。
求解一个随机场,就是要找到有多少种不同的样本空间,以及其中随机变量的概率分布。
马尔可夫随机场
马尔科夫随机场是典型的马尔科夫网,这是一种著名的无向图模型。图中每个节点表示一个或一组变量,结点之间的边表示两个变量之间的依赖关系。马尔科夫随机场有一组势函数,亦称为“因子”,这是定义在变量子集上非负实函数,主要用于定义概率分布函数。
图-1显示出一个简单的马尔科夫随机场。对于图中结点的一个子集,若其中任意两点间都有边连接线,则称该结点子集为一个“团”。若在一个团中加入另外任何一个节点都不再形成团,则称该团为“极大团”;换言之,极大团就是不再被其他团所包含的团。例如在图-1中,{x1,x2},{x1,x3},{x2,x4},{x2,x5},{x2,x6},{x3,x5},{x5,x6}和{x2,x5,x6}都是团,并且除了{x2,x5},{x2,x6}和{x5,x6}之外都是极大团;但是,因为x2和x3之间缺乏连接,{x1,x2,x3}并不构成团。显然,每个节点至少出现在一个极大团中。
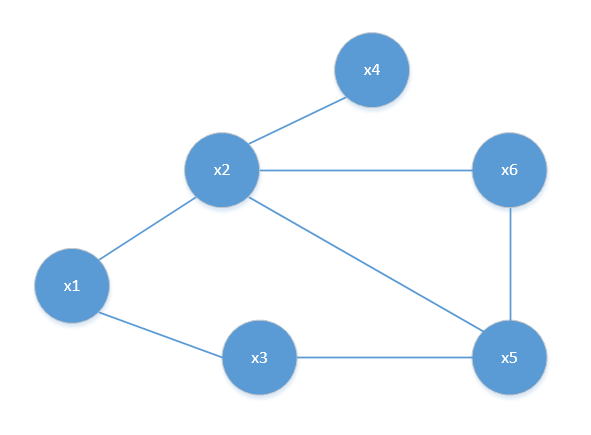
图-1 一个简单的马尔科夫随机场
在马尔科夫随机场中,多个变量之间的联合概率分布能基于团分解为多个因子的乘积,每个因子仅于一个团相关。具体来说,对于n个变量$x={x_1,x_2···x_n}$,所有团构成的集合为C,与团$Q∈C$对应的变量集合记为$x_Q$,则联合概率p(x)定义为
\(P(x)= \frac{1}{Z}∏_{Q∈C}ψ_Q(x_Q)\) 式-1
其中$ψ_Q$为与团Q对应的势函数,用于对团Q中的变量关系进行建模,$ Z= \sum_x ∏_{Q∈C}ψ_Q(x_Q)$为规范化因子,以确保P(x)是被正确定义的概率。在实际应用中,精确计算Z通常很困难,但许多任务往往并不需获得Z的精确值。
条件随机场
条件随机场(Confitional Random Field,简称CRF)是一种判别式无向图模型,生成模型是直接对联合分布进行建模,而判别式模型则是对条件分布进行建模。隐马尔科夫和马尔科夫随机场都是生成式模型,而条件随机场则是判别式模型。
条件随机场试图对多个变量在给定观测值后的条件概率进行建模。具体来说,若令$x={x_1,x_2···x_n}$为观察序列,$y={y_1,y_2···y_n}$为与之相应的标记序列。则条件随机场的目标是构建条件概率模型$P(y \mid x)$。需要注意的是,标记变量y可以是结构型变量,即分量之间具有某种相关性。例如在自然语言处理的词性标注任务中,观测数据为语句(即单词序列),标记为相应的词性序列,具有线性序列结构。如图-2所示。
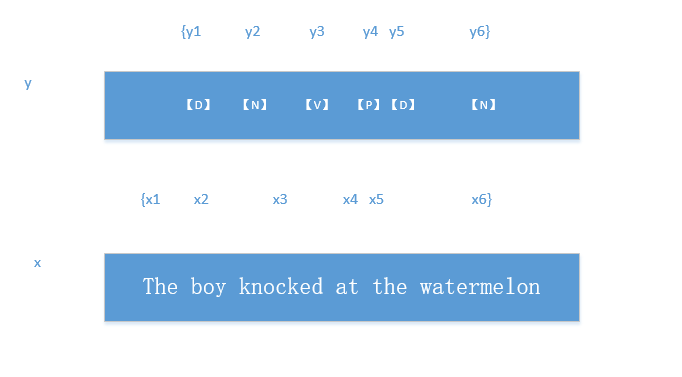
图-2
令$G=<V,E>$表示结点与标记变量y中元素一一对应的无向图,$y_v$表示与结点v对应的标记变量,$n(v)$表示结点v的邻接结点,若图G的每个变量$y_v$都满足马尔科夫性,即
\(P(y_v \mid x,Y_{V \ v} )=P(y_v \mid x,Y_{n(v)})\),
则$(y,x)$构成一个条件随机场
理论上来说,图G可具有任意结构,只要能表示标记变量之间的条件独立性关系即可。但在现实应用中,尤其是对标记序列建模时,最常用的仍是图-3所示的链式结构,即“链式条件随机场”。下面我们主要讨论这种条件随机场。
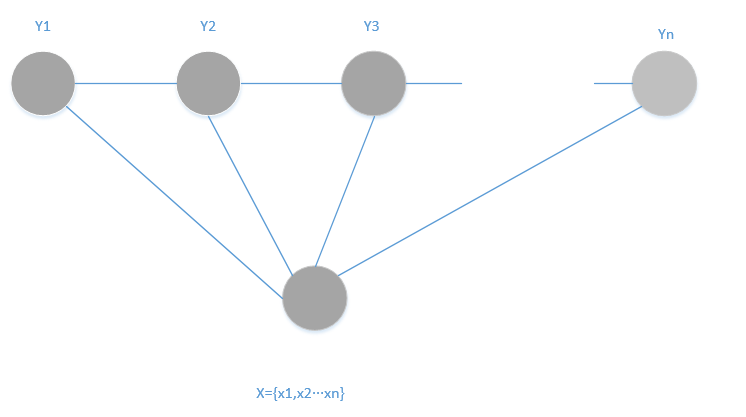
图-3链式条件随机场的图结构
链式条件随机场
与马尔科夫随机场定义联合概率的方式类似,条件随机场使用势函数和图结构上的团来定义条件概率$P(y \mid x)$。给定观测序列x,图-3所示的链式条件随机场主要包含两种关于标记变量的团,即单个标记变量${y_i}$以及相邻的标记变量${y_{i-1},y_i}$。选择合适的势函数,即可得到形如式-1的条件概率定义。在条件随机场中,通过选用指数势函数并引入特征函数,条件概率被定义为
\(P(y \mid x)=\frac{1}{z}exp(\sum_j \sum_{i=1}^{n-1}λ_jt_j(y_{i+1},y_i,x,i)+\sum_k\sum_{i=1}^nυ_kδ_k(y_i,x,i))\) 式-2
其中$t_j(y_{i+1},y_i,x,i)$是定义在观测序列的两个相邻标记位置上转移特征函数,用于刻画相邻标记变量之间的相关关系以及观测序列对它们的影响,$δ_k(y_i,x,i)$是定义在观测序列的标记位置i上的状态特征函数,用于刻画观测序列对标记变量的影响,$λ_j$和$υ_k$为参数,Z为规划化因子,用于确保式-2是正确定义的概率。
显然要是用条件随机场,还需定义合适的特征函数。特征函数通常是实值函数,以刻画数据的一些很可能成立或期望成立的经验特性。以图-1所示的词性标注任务为例,若采用转移特征函数
\[t_j(y_{i+1},y_i,x,i)=\begin{cases}1,&if \quad y_{i+1}=[P],y_i=[V] \quad and \quad x_i='knock'\\ 0, &otherwise \end{cases}\]则表示第i个观测值$x_i$为单词’knock’时,相应的标记$y_i$和$y_{i+1}$很可能分别为[v]和[P]。若采用状态特征函数
\[δ_k(y_i,x,i)=\begin{cases}1,&if \quad y_{i}=[V]and\quad x_i='knock'\\ 0, &otherwise \end{cases}\]则表示观测值$x_i$为单词’knock’时,它所对应的标记很可能成为[v]。
Viterbi预测算法
条件随机场的预测问题是给定义条件随机场$P(y \mid x)$和输入序列(观测序列)x,求条件概率最大的输出序列(标记序列)y*,即对观测序列进行标注。
\[y*=arg \max_{y}P_w(y \mid x)\] \[\quad =arg \max_y\frac{exp(w·F(y,x))}{Z}\] \[\quad =arg \max_y exp(w·F(y,x))\] \[\quad =arg \max_y (w·F(y,x))\]于是,条件随机场的预测问题成为求非规范化概率最大的最优路径问题
\[max_y \sum^n _{i=1}w·F_i(y_{i-1},y_i,x)\] \[F_i(y_{i-1},y_i,x)=(f_1(y_{i-1},y_i,x,i),f_2(y_{i-1},y_i,x,i)····f_k(y_{i-1},y_i,x,i))^T\]根据维特比算法进行求解
条件随机场预测的维特比算法
输入:模型特征向量$F(x,y)$和权值向量w,观测序列$x=(x_1,x_2···,x_n)$
输出:最优路径
\[y^*=(y_1^*,y_2^*···y_n^*)\](1)初始化
\[δ_1(j)=w·F_1(y_0=start,y_1=j,x), j=1,2···m\](2)递推,对i=1,2,3,···n
\[δ_i(l)=\max_{1≤j≤m}{δ_{i-1}(j)+w·F_i(y_{i-1}=j,y_i=l,x)} \quad l=1,2···m\] \[ψ_i(l)=arg \max_{1≤j≤m}{δ_{i-1}(j)+w·F_i(y_{i-1}=j,y_i=l,x)} \quad l=1,2···m\](3)终止
\(\max_y(w·F(y,x))=\max_{1≤j≤m}δ_n(j)\)λ
\[y^*_n=arg \max_{1≤j≤m}δ_n(j)\](4)返回路径
\[y*_i=ψ_{i+1}(y*_{i+1}), i=n-1,n-2,···1\]求最优路径\(y*=(y*_1,y*_2···,y*_n)\)
例子
设有一标注问题:输入观测序列为$x=(x_1,x_2,x_3)$,输出标记序列为$y=(y_1,y_2,y_3)$,$y_1,y_2,y_3$取值为1,2。
假设特征函数$t_j,s_k$和对应的权值$λ_j,μ_k$如下:
\[\begin{align}t_1&=t_1(y_{i-1}=1,y_i=2,\mathbb{x},i),\quad i=2,3,\quad\lambda_1=1\\t_2&=t_2(y_1=1,y_2=1,\mathbb{x},2),\quad\lambda_2=0.6\\t_3&=t_3(y_2=2,y_3=1,\mathbb{x},3),\quad\lambda_3=1\\t_4&=t_4(y_1=2,y_2=1,\mathbb{x},2),\quad\lambda_4=1\\t_5&=t_5(y_2=2,y_3=2,\mathbb{x},3),\quad\lambda_5=0.2\\\\s_1&=s_1(y_1=1,\mathbb{x},1),\quad\mu_1=1\\s_2&=s_2(y_i=2,\mathbb{x},i),\quad i=1,2\quad\mu_2=0.5\\s_3&=s_3(y_i=1,\mathbb{x},i),\quad i=2,3\quad\mu_3=0.8\\s_4&=s_4(y_3=2,\mathbb{x},3),\quad\mu_4=0.5\end{align} %]]>\]以$t_1$为例,其他特征函数类似:
\[t_1(y_{i-1},y_i,\mathbb{x},i)=\begin{cases}1,&y_{i-1}=1,y_i=2,\mathbb{x},i,(i=2,3)\\0,&其他\end{cases} %]]>\]现用维特比算法求解最可能的标记序列: 1.初始化
\[i=1:δ_1(j)=w·F_1(y_0=start,y_1=j,x),j=1,2\] \[δ_1(1)=μ_1s_1=1,δ_1(2)=μ_2s_2=0.5\]2.递推
\[i=2: δ_2(l)=max_jδ_1(j)+w·F_2(j,l,x)\] \[\begin{align}\delta_2(1)&=\max\{\delta_1(1)+\mathbb{w}\cdot F_2(y_1=1,y_2=1,\mathbb{x}),\delta_1(2)+\mathbb{w}\cdot F_2(y_1=2,y_2=1,\mathbb{x})\}\\&=\max\{1+\lambda_2t_2+\mu_3s_3,0.5+\lambda_4t_4+\mu_3s_3\}=2.4,\quad\Psi_2(1)=1\end{align} %]]>\] \[\begin{align}\delta_2(2)&=\max\{\delta_1(1)+\mathbb{w}\cdot F_2(y_1=1,y_2=2,\mathbb{x}),\delta_1(2)+\mathbb{w}\cdot F_2(y_1=2,y_2=2,\mathbb{x})\}\\&=\max\{1+\lambda_1t_1+\mu_2s_2,0.5+\mu_2s_2\}=2.5,\quad\Psi_2(2)=1\end{align} %]]>\] \[i=3: δ_3(l)=max_jδ_2(j)+w·F_3(j,l,x)\] \[\begin{align}\delta_3(1)&=\max\{\delta_2(1)+\mathbb{w}\cdot F_3(y_2=1,y_3=1,\mathbb{x}),\delta_2(2)+\mathbb{w}\cdot F_3(y_2=2,y_3=1,\mathbb{x})\}\\&=\max\{2.4+\mu_3s_3,2.5+\lambda_3t_3+\mu_3s_3\}=4.3,\quad\Psi_3(1)=2\end{align} %]]>\] \[\begin{align}\delta_3(2)&=\max\{\delta_2(1)+\mathbb{w}\cdot F_3(y_2=1,y_3=2,\mathbb{x}),\delta_2(2)+\mathbb{w}\cdot F_3(y_2=2,y_3=2,\mathbb{x})\}\\&=\max\{2.4+\mu_4s_4,2.5+\lambda_5t_5+\mu_4s_4\}=3.2,\quad\Psi_3(2)=1\end{align} %]]>\]3.终止
\[\max_y(w·F(y,x))=max \delta_3(l)=\delta_3(1)=4.3\] \[y^*_{3}=arg \max_l\delta_3(l)=1\]4.返回
\[\begin{gather}y_2^*=\Psi_3(y_3^*)=\Psi_3(1)=2\\y_1^*=\Psi_2(y_2^*)=\Psi_2(2)=1\end{gather}\]所以最优标记序列为
\[y^*=(y^*_1,y^*_2,y^*_3)=(1,2,1)\]