1.概述
什么是卷积
整篇博客都会探讨这个问题,但先把握行文脉络很有帮助。那么粗略来讲,什么是卷积呢?
你可以把卷积想象成一种混合信息的手段。想象一下装满信息的两个桶,我们把它们倒入一个桶中并且通过某种规则搅拌。也就是说卷积是一种混合两种信息的流程。
卷积也可以形式化地描述,事实上,它就是一种数学运算,跟加减乘除没有本质的区别。虽然这种运算本身很复杂,但它非常有助于简化更复杂的表达式。在物理和工程上,卷积被广泛地用于化简等式———等会儿简单地形式化描述卷积后———我们将把这些领域的思想和深度学习联系起来,以加深对卷积的理解。但现在我们先从实用的角度理解卷积。
我们如何对图像应用卷积
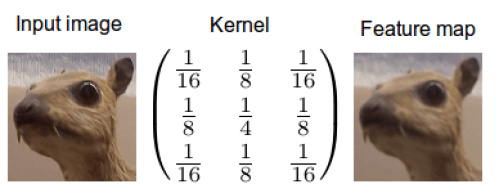
当我们在图像上应用卷积时,我们在两个维度上执行卷积———水平和垂直方向。我们混合两桶信息:第一桶是输入的图像,由三个矩阵构成———RGB三通道,其中每个元素都是0到255之间的一个整数。第二个桶是卷积核,单个浮点数矩阵。可以将卷积核的大小和模式想象成一个搅拌图像的方法。卷积核的输出是一幅修改后的图像,在深度学习中经常被称作feature map。对每个颜色通道都有一个feature map。
卷积神经网络是一种经典的前馈神经网络,主要受生物中的感受野的概念提出的,一个神经元由特定区域控制,只有这个特定区域才能激活该神经元,包括正向传播和反向传播两个过程。正向传播是输入信号从输入层,经过若干层,从输出层输出的过程:反向传播是将误差信号从输出层反向传播至输入层的过程。反向传播主要使用误差后向传播(EBP)算法和梯度下降对网络各层调整权重,通过比较输出信号和期望信号得到误差信号,利用链式求导将误差信号逐层向前得到各层误差信号,根据各层误差信号调整各层权重和相关参数,调整权重和相关参数的过程就是训练学习的过程。
卷积神经网络结构一般包括卷积层(Convolution层)、下采样层(Pooling层)和全连接层(Fully-Connection层):下采样层一般连接在卷积层之后,与卷积层交替出现,最后连接全连接层。卷积神经网络采用局部连接、权值共享和空间或时间相关下采样方法,从而获得很好的平移、缩放和扭曲不变性,使提取的特征更具有区分性。下图是一个卷积神经网络的示意图。
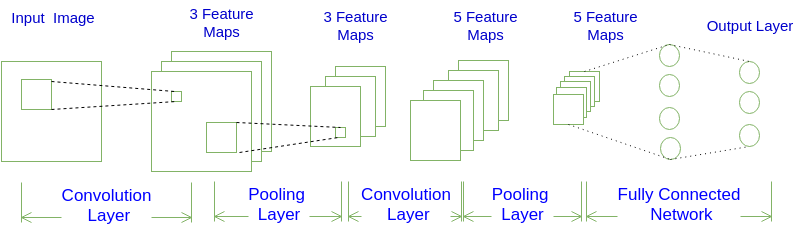
对于上图展示的神经网络,我们看到输入层的宽度和高度对应于输入图像的宽度和高度,而它的深度为1。接着第一个卷积层对这幅图像进行了卷积操作,得到了三个Feature Map。这里的“3”就是这个卷积层包含三个Filter,也就是三套参数,每个Filter都可以把原始输入图像卷积得到一个Feature Map,三个Filter就可以得到三个Filter Map。至于一个卷积层可以有多少个Filter,那是可以自由设定的。也就是说,卷积层的Filter个数也是一个超参数。我们可以把Feature Map可以看做是通过卷积变换提取到的图像特征,三个Filter就对原始图像提取出三组不同的特征,也就是得到了三个Feature Map,也称三个通道。
接着观察上图,在第一个卷积层之后,Pooling层对三个Feature map 做了下采样,得到了三个更小的Feature Map。接着,是第二个卷积层,它有5个Filter。每个Filter都把前面下采样之后的3个Feature Map卷积在一起,得到一个新的Feature Map。这样,5个Filter就得到了5个Feature Map。接着,是第二个Pooling层,继续对5个Feature Map进行下采样,得到了5个更小的Feature Map。
上图所示网络的最后两层是全连接层。第一个全连接层的每个神经元,和上一层5个Feature Map中的每个神经元相连,第二个全连接层(也就是输出层)的每个神经元,则和第一个全连接层的每个神经元相连,这样得到了整个网络的输出。
为什么机器学习中图像卷积有用
图像中可能含有很多我们不关心的噪音。一个好例子是我和Jannek Thomas在Burda Bootcamp做的项目。Burda Bootcamp是一个让学生像黑客马拉松一样在非常短的时间内创造技术风暴的实验室。与9名同事一起,我们在2个月内做了11个产品出来。其中之一就是针对时尚图像用深度编码器做的搜索引擎:你上传一幅时尚服饰的图片,编码器自动找出类似的服饰。
如果你想要区分衣服的式样,那么衣服的颜色就不那么重要了;另外像商标之类的细节也不那么重要。最重要的可能是衣服的外形。一般来讲,女装衬衫的形状与衬衣、夹克和裤子的外观非常不同。如果我们过滤掉这些多余的噪音,那我们的算法就不会因为颜色、商标之类的细节分心了。我们可以通过卷积轻松地实现这项处理。
我的同事Jannek Thomas通过索贝尔边缘检测滤波器(与上上一幅图类似)去掉了图像中除了边缘之外的所有信息———这也是为什么卷积应用经常被称作滤波器而卷积核经常被称作滤波器(更准确的定义在下面)的原因。由边缘检测滤波器生成的feature map对区分衣服类型非常有用,因为只有外形信息被保留下来。
彩色的左上角是搜索query,其他是搜索结果,你会发现自动编码器真的只关注衣服的外形,不是颜色。
再进一步:有许多不同的核可以产生多种feature map,比如说锐化图像(强调细节),或者模糊图像(减少细节),并且每个feature map 都可能帮助算法作出决策(一些细节,比如衣服上有3个纽扣而不是两个,可能可以区分一些服饰)。
使用这种手段——读入输入,输入变换,然后把feature map喂给某个算法——被称为工程。特征工程非常难,很少有资料帮你上手。造成的结果是,很少有人能熟练地在多个领域应用特征工程。特征工程师——纯手工——也是Kaggle比赛中的最重要的技能。特征工程这么难的原因是,对于每种数据每种问题,有用的特征都是不同的,图像类任务的特征可能对时序类任务不起作用;即使两个任务都是图像类的,也很难找出相同的有效特征,因为示待的物体不同,有用的特征也不同。这非常依赖经验。
所以特征工程对新手来讲特别困难。不过对图像而言,是否可用利用卷积核自动找出某个任务中最适合的特征?
进入卷积神经网络
卷积神经网络就是干这个的。不同于刚才使用固定数字的卷积核,我们赋予参数给这些核,参数将在数据上得到训练。随着卷积神经网络的训练,这些卷积核为了得到有用的信息,在图像或feature map 上的过滤工作会变得越来越好。这个过程是自动的,称作特征学习。特征学习自动适配新的任务;我们只需在新数据上训练一下自动找出新的过滤器。这是卷积神经网络如此强大的原因——不需要繁重的特征工程了!
通常卷积神经网络并不是单一的核,而是同时学习多层级的多个核。比如一个32×16×16的核用到256×256的图像上去会产生32个241×241(image size -kernel size+1)的feature map。所以自动地得到了32个有用的新特征。这些特征可以作为下个核的输入。一旦学习到多级特征,我们简单地将它们传给一个全连接的简单的神经网络,由它完成分类。这就是概念上理解卷积神经网络所需的全部知识。
2.高级概念
我们现在对卷积有了一个良好的初步认识,也知道了卷积神经网络在干什么、为什么它如此强大。现在让我们深入了解一下卷积运算中到底发生了什么。我们将认识到刚才对卷积的讲解是粗浅的,并且这里有更优雅的解释。通过深入理解,我们可以理解卷积的本质并将其应用到许多不同的数据上去。万事开头难,第一步理解卷积原理。
卷积定理
要理解卷积,不得不提convolution theorem,它将时域和空域上的复杂卷积对应到了频域中的元素间简单的乘积。这个定理非常强大,在许多科学领域中得到了广泛应用。卷积定理也是快速傅里叶变换算法被称为20世纪最重要的算法之一的一个原因。 \(h(x)=f\otimes g=\int_{-\infty}^{\infty}f(x-u)g(u)du=F^{-1}\big(\sqrt{2\pi}F[f]F[g]\big)\) \(\begin{align}\text{feature map}&=\text{input}\otimes \text{kernel}\\&=\sum_{y=0}^{\text{columns}}\Bigg(\sum_{x=0}^{\text{rows}}\text{input}(x-a,y-b)\text{kernel}(x,y)\Bigg)\\&=F^{-1}\big(\sqrt{2\pi}F[\text{input}]F[\text{kernel}]\big)\end{align}\)
第一个等式是一维连续域上两个连续函数的卷积;第二个等式是二维离散域(图像)上的卷积。这里 ⊗ 指的是卷积,F 指的是傅里叶变换,$F^{-1}$ 表示傅里叶逆变换,$\sqrt{2\pi}$ 是一个正规化常量。这里的“离散”指的是数据由有限个变量构成(像素);一维指的是数据是一维的(时间),图像则是二维的,视频则是三维的。
为了更好地理解卷积定理,我们还需要理解数字图像处理中的傅里叶变换。
快速傅里叶变换
快速傅里叶变换是一种将时域和空域中的数据转换到频域上去的算法。傅里叶变换用一些正弦和余弦波的和来表示原函数。必须注意的是,傅里叶变换一般涉及到复数,也就是说一个实数被变换为一个具有实部和虚部的复数。通常虚部只在一部分领域有用,比如将频域变换回到时域和空域上;而在这篇博客里会被忽略掉。你可以在下面看到一个信号(一个以时间为参数的有周期的函数通常称为信号)是如何被傅里叶变换的:
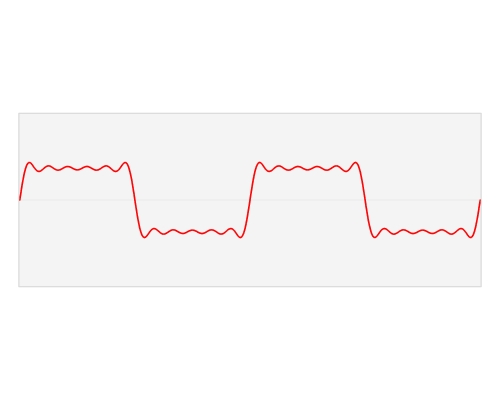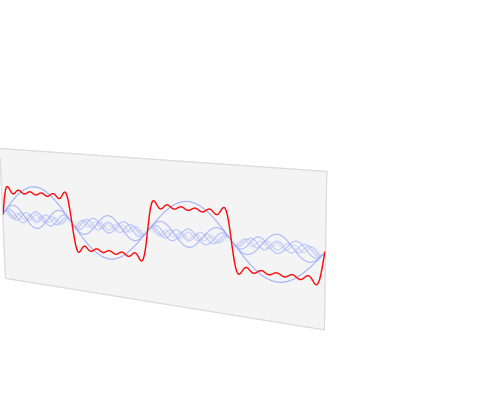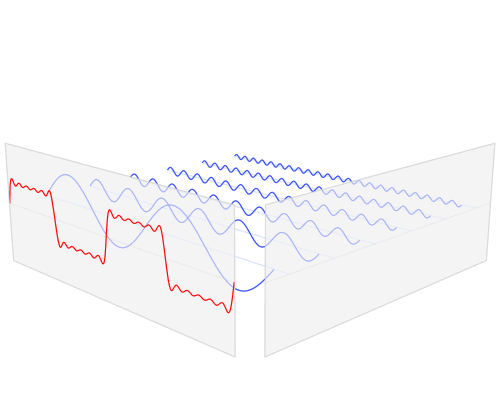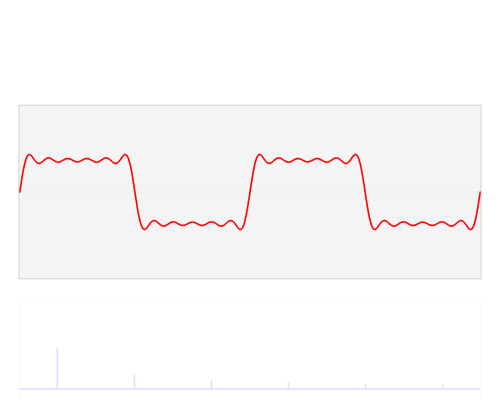
红色是时域,蓝色为频域
傅里叶域上的图像

我们如何想象图像的频率呢?想象一张只有两种模式的纸片,现在把纸片竖起来顺着线条的方向看过去,就会看到一个一个的亮点。这些以一定间隔分割黑白部分的波就代表这频率。在频域中,低频率更接近中央而高频率更接近边缘。频域中高强度(亮度、白色)的位置代表着原始图像亮度改变的方向。这一点在接下来这张图与其对数傅里叶便函(对傅里叶变换的实部取对数,这样可以减小亮度的差别,便于观察更广的亮度区域)中特别明显:

我们马上就可以发现傅里叶便换包含关于物体朝向的信息。如果物体被旋转了一个角度,从图像像素上可能很难判断,但从频域上可以很明显地看出来。
这个很重要的启发,基于傅里叶定理,我们知道卷积神经网络在频域上检测图像并且捕捉了物体的方向信息。于是卷积神经网络就比传统算法更擅长处理旋转后的图像(虽然还是比不上人类)。
频率过滤与卷积
为什么卷积经常被描述为过滤,为什么卷积核经常被称为过滤器呢?通过下一个例子可以解释:
如果我们对图像执行傅里叶变换,并且乘以一个圆形(背景填充黑色,也就是0),我们可以过滤掉所有的高频值(它们会成为0,因为填充是0)。注意过滤后的图像依然有条纹模式,但图像质量下降了很多——这就是jpeg压缩算法的工作原理(虽然有些不同但用了类似的变换),我们变换图形,然后只保留部分频率,最后将其逆变换为二维图片;压缩率就是黑色背景与圆圈的比率。
我们现在将圆圈想象为一个卷积核,然后就有了完整的卷积过程——就像在卷积神经网络中看到的那样。要稳定快速地执行傅里叶变换还需要许多技巧,但这就是基本理念了。
现在我们已经理解了卷积定理和傅里叶变换,我们可以将这些理念应用到其他科学领域,以加强我们对深度学习中的卷积的理解。
流体力学的启发
流体力学为空气和水创建了大量的微分方程模型,傅里叶变换不但简化了卷积,也简化了微分,或者说任何利用了微分方程的领域。有时候得到解析解的唯一方法就是对微分方程左右同时执行傅里叶变换。在这个过程中,我们常常将解写成两个函数卷积的形式,以得到更简单的表达。这是在一个维度上的应用,还有在两个维度上的应用,比如天文学。
扩散
你可以混合两种液体(牛奶和咖啡),只要施加一个外力(汤勺搅拌)——这被称为对流,而且是个很快的过程。你也可以耐心等待两种液体自然混合——这被称为扩散,通常是很慢的过程。
想象一下,一个鱼缸被一块板子隔开,两边各有不同浓度的盐水。抽掉板子后,两边的盐水会逐步混合为同一个浓度。浓度差越大,这个过程越剧烈。
现在想象一下,一个鱼缸被 256×256 个板子分割为 256×256 个部分(这个数字似乎不对),每个部分都有不同浓度的盐水。如果你去掉所有的挡板,浓度类似的小块间将不会有多少扩散,但浓度差异大的区块间有巨大的扩散。这些小块就是像素点,而浓度就是像素的亮度。浓度的扩散就是像素亮度的扩散。
这说明,扩散现象与卷积有相似点——初始状态下不同浓度的液体,或不同强度的像素。为了完成下一步的解释,我们还需要理解传播子。
理解传播子
传播子就是密度函数,表示流体微粒应该往哪个方向传播。问题是神经网络中没有这样的概率函数,只有一个卷积核——我们要如何统一这两种概念呢?
我们可以通过正规化来讲卷积核转化为概率密度函数。这有点像计算输出值的softmax。下面就是对第一个例子中的卷积核执行的softmax结果:
\[Z=\text{softmax}\Bigg[\begin{pmatrix} -1&-1&-1\\-1&8&-1\\-1&-1&-1 \end{pmatrix}\Bigg]=\begin{pmatrix} 0.0001&0.0001&0.0001\\0.0001&0.9992&0.0001\\0.0001&0.0001&0.0001 \end{pmatrix}\] 现在我们就可以从扩散的角度来理解图像上的卷积了。我们可以把卷积理解为两个扩散流程。首先,当像素亮度改变时(黑色到白色等)会发生扩散;然后某个区域的扩散满足卷积核对应的概率分布。这意味着卷积核正在处理的区域中的像素点必须按照这些概率来扩散。
在上面那个边缘检测器中,几乎所有临近边缘的信息都会聚集到边缘上(这在流体扩散中是不可能的,但这里的解释在数学上是成立的)。比如说所有低于 0.00010.0001 的像素都非常可能流动到中间并累加起来。与周围像素区别最大的区域会成为强度的集中地,因为扩散最剧烈。反过来说,强度最集中的地方说明与周围对比最强烈,这也就是物体的边缘所在,这解释了为什么这个核是一个边缘检测器。
所以我们就得到了物理解释:卷积是信息的扩散。我们可以直接把这种解释运用到其他核上去,有时候我们需要先执行一个 softmax 正规化才能解释,但一般来讲核中的数字已经足够说明它想要干什么。比如说,你是否能推断下面这个核的的意图?
\[Z=\text{softmax}\Bigg[\begin{pmatrix} \frac{1}{16}&\frac{1}{8}&\frac{1}{16}\\\frac{1}{8}&\frac{1}{4}&\frac{1}{8}\\\frac{1}{16}&\frac{1}{8}&\frac{1}{16} \end{pmatrix}\Bigg]=\begin{pmatrix} 0.105&0.1125&0.105\\0.1125&0.13&0.1125\\0.105&0.1125&0.105 \end{pmatrix}\]3.总结
这篇博客中我们知道了卷积是什么、为什么在深度学习中这么有用。图片区块的解释很容易理解和计算,但有其理论局限性。我们通过学习傅里叶变换知道傅里叶变换后的时域上有很多关于物体朝向的信息。通过强大的卷积定理我们理解了卷积是一种在像素间的信息流动。
个人来讲,我觉得写这篇博客很有趣。曾经很长一段时间我都觉得本科的数学和统计课是浪费时间,因为它们太不实用了(哪怕是应用数学)。但之后——就像突然中大奖一样——这些知识都相互串起来了并且带了新的理解。我觉得这是个绝妙的例子,启示我们应该耐心地学习所有的大学课程——哪怕它们一开始看起来没有用。