循环和递归
循环神经网络(recurrent nerual network)或RNN是一类用于处理序列数据的神经网络。就像卷积网络是专门处理网络化数据X(如一个图像)的神经网络，循环神经网络是专门用于处理序列$x^{1},···,x^{r}$的神经网络。正如卷积网络可以很容易地扩展到具有很大宽度和高度的图像，以及处理大小可变的图像，循环网络可以扩展到更长的序列(比不基于序列的特化网络长得多)。大多数循环网络也能处理可变长度的序列。
从多层网络出发到循环网络，我们需要利用上世纪80年代机器学习和统计模型早期思想的优点：在模型的不同部分共享参数。参数共享使得模型能够扩展到不同形式的样本(这里指不同长度的样本)并进行泛化。如果我们在每个时间点都有一个单独的参数，我们不但不能泛化到训练时没有见过序列的长度，也不能在时间上共享不同序列长度和不同位置的统计强度。当信息的特定部分会在序列内多个位置出现时，这样的共享尤为重要。例如，考虑这两句话：“I want to Nepal in 2009”和“In 2009, I went to Nepal.”如果我们让一个机器学习模型读取这两个句子，并提取叙述者去Nepal的年份，无论“2009年”作为相关资料片段。假设我们要训练一个处理固定长度句子的前馈网络。传统的全连接前馈网络会给每个输入特征分配一个单独的参数，所以需要分别学习句子每个位置的所有语言规则。相比之下，循环神经网络在几个时间布内共享相同的权重，不需要分别学习句子每个位置的所有语言规则。
为简单起见，我们说的RNN是指在序列上的操作，并且该序列在时刻t（从1到r）包含向量$x^{t}$。在实际情况中，循环网络通常在序列的小批量操作，并且小批量的每项具有不同的序列长度$r$。我们省略了小批量索引来简化记号。此外，时间步索引不必是字面上现实世界中流逝的时间。有时，它仅表示序列中的位置。RNN也可以应用于跨越两个维度的空间数据（如图像）。当应用于涉及时间的数据，并且将整个序列提供给网络之前就能观察到整个序列时，该网络可具有关于时间向后的连接。
展开计算图
计算图是形式化一组计算结构的方式，如那些涉及将输入和参数映射到输出和损失的计算。本节，我们对展开递归或循环计算得到的重复结构进行解释，这些重复结构通常对应于一个事件链。展开这个计算图将导致深度网络结构中的参数共享。
例如，考虑动态系统的经典形式：
\[s^{(t)}=f(s^{(t-1)};θ)\quad 式(1)\]其中，$s^{(t)}$称为系统的状态。
s在时刻t的定义需要参考时刻t-1时的同样的定义，因此式(1)是循环的。
对有限时间$\tau,\tau-1$次应用这个定义可以展开这个图。如$\tau=3$,我们对式(1)展开，可以得到：
\(\begin{align}\boldsymbol{s}^{(3)} &= f(\boldsymbol{s}^{(2)};\boldsymbol{\theta}) \quad 式(2)\\&= f(f(\boldsymbol{s}^{(1)};\boldsymbol{\theta});\boldsymbol{\theta})\quad 式(3)\end{align}\)
以 这种方式重复应用定义，展开等式，就能得到不涉及循环的表达。现在我们可以使用传统的有向无环计算图呈现这样的表达。
式(2)和式(3)的展开计算图如下图所示。
上图中，将式(1)描述的经典动态图表示为展开的计算图。每个节点表示在某个时刻t的状态，并且函数f将t处的状态映射到t+1处的状态。所有事件步都使用相同的参数(用于参数f的相同θ值)。
作为另一个例子，让我们考虑外部信号$x^{(t)}$驱动的动态系统，
\(s^{(t)}=f(s^{(t-1)},x^{t};θ)\)
我们可以看到，当前状态包含了整个过去序列的信息。
循环神经网络可以通过许多不同的方式建立。就像几乎所有函数都可以被认为是前馈网络，本质上任何涉及循环的函数都可以被认为是一个循环神经网络。
很多循环神经网络使用下式或类似的公式定义隐藏单元的值。为了表明状态是网络的隐藏单元，我们使用变量h代表状态重写上式：
\(h^{t}=f(h^{(t-1)},x^{t};θ)\)
如下图所示，典型RNN会增加额外的架构特性，如读取状态信息h进行预测的输出层。
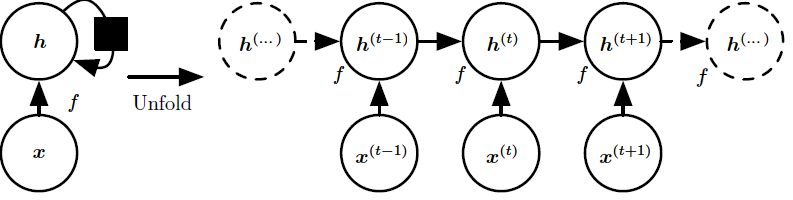
如上图，没有输出的循环网络。此循环网络只处理来自输入x的信息，将其合并到经过时间向前传播的状态h。(左)回路原理图。黑色方块表示单个时间步的延迟。(右)同一网络被视为展开的计算图，其中每个节点现在与一个特定的时间实例相关联。
- 当训练循环网络根据过去预测未来时，网络通常要学会使用$h^{t}$作为过去序列(直到t)与任务相关方面的有损摘要。此摘要一般而言一定是有损的，因为其映射任意长度的序列$(x^{t},x^{t-1}···,x^2,x^1)$到一固定长度的向量$h^{t}$。根据不同的训练准则，摘要可能选择性地精确保留过去序列的某些方面。例如，如果在统计语言建模中使用的RNN，通常给定前一个词预测下一个词，可能没有必要存储时刻t前输入序列中的所有信息；而仅仅存储足够预测句子其余部分的信息。最苛刻的情况是我们要去$h^{t}$足够丰富，并能大致恢复序列。
上式可以用不同的方式绘制。一种方法是为可能在模型的物理实现中存在的部分赋予一个节点，如生物神经网络。在这个观点下，网络定义了实时操作的回路，如式(2)的左侧，其当前状态可以影响其未来的状态。在本章中，我们使用回路图的黑色方块表示在时刻t的状态到时刻$t+1$的状态单个时刻延迟中的相互作用。另一个绘制RNN的方法是展开的计算图，其中每个组件由许多不同的变量表示，每个时间步一个变量，表示在该时间点组件的状态。每个时间步的每个变量绘制为计算图的一个独立节点，如上图的右侧。我们所说的展开是将左图中的回路映射为右图中包含重复组件的计算图的操作。目前，展开图的大小取决于序列的长度。
我们可以用一个函数$g^{(t)}$代表经t步展开后循环:
\(\begin{align} h^{(t)}&=g^{t}(x^{(t)},x^{(t-1)},···x^{(2)},x^{(1)})\\&=f(h^{(t-1)},x^{(t)};θ)\end{align}\)
函数$g^{(t)}$将全部的过去序列$(x^{t},x^{t-1},···,x^{2},x^{1})$作为输入来生成当前状态，但是展开的循环架构允许我们将$g^{(t)}$分解为函数f的重复应用。因此，展开过程引入两个主要优点：
- 无论序列的长度，学成的模型始终具有相同的输入大小，因为它指定的是从一种状态到另一种状态的转移，而不是在可变长度的历史状态上长度。
- 我们可以在每个时间步使用相同参数的相同转移函数f。
循环神经网络
基于上节中的图展开和参数共享的思想，我们可以设计各种循环神经网络。
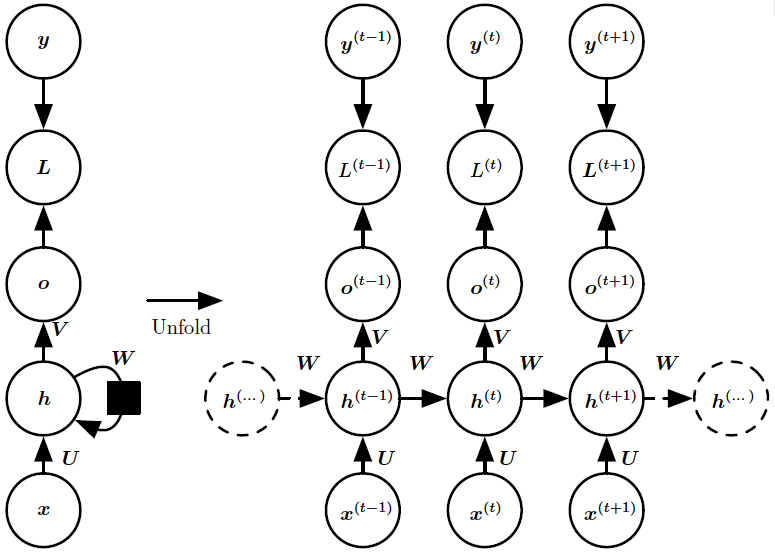
如上图1示，计算循环网络(将x值的输入序列映射到输出值ο的对应序列)训练损失的计算图。损失L衡量每个ο与相应的训练目标y的距离。当使用softmax输出时，我们假设ο是未归一化的对数概率。损失L 内部计算$\hat{\boldsymbol{y}} = \text{softmax}(\boldsymbol{o})$，并将其与目标$y$比较。RNN输入到隐藏的连接由权重矩阵$U$参数化，隐藏到隐藏的循环连接由权重矩阵$V$参数化。（左）使用循环连接绘制的RNN和它的损失，(右)同一网络被视为展开的计算图，其中每个节点现在与一个特定的时间实例相关联。
循环神经网络中一些重要的设计模式包括以下几种：
- 每个时间步都有输出，并且隐藏单元之间有循环连接的循环网络，如上图1所示。
- 每个时间步产生一个输出，只有当前时刻的输出到下个时刻的隐藏单元之间有循环连接的循环网络，如下图2所示。
- 隐藏单元之间存在循环连接，但读取整个序列产生单个输出的循环网络， 如下图3所示。
图2，此类RNN的唯一循环是从输出到隐藏层的反馈连接。在每个时间步t,输出为$x_t$，隐藏层激活为$h^{t}$,输出为$o^{t}$，目标为$y^{t}$，损失为$L^{t}$。(左)回路原理图。(右)展开的计算图。这样的RNN没有上图1表示的RNN那样强大(只能表示更小的函数集合)。图1中RNN可以选择将其想要的关于过去的任何信息放入隐藏表示h中并且将h传播到未来。该图中的RNN被训练为将特定输出值放入$ο$中，并且$o$是允许传播到未来的唯一信息。此处没有从$h$前向传播的直接连接。之前的$h$仅通过产生的预测间接地连接到当前。$o$通常缺乏过去的重要信息，除非它非常高维且内容丰富。这使得该图中的RNN不那么强大，但是它更容易训练，因为每个时间步可以与其他时间步分离训练，允许训练期间更多的并行化。
任何图灵可计算的函数都可以通过这样一个有限维的循环网络计算。RNN经过若干时间步后读取输出，这与由图灵机所用的时间步是渐近线性的，与输入长度也是渐近线性的。
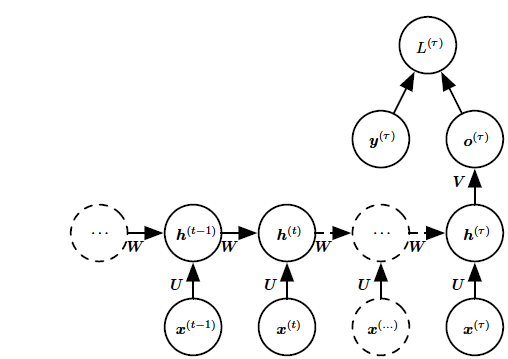
图3，关于时间展开的循环神经网络，在序列结束时具有单个输出。这样的网络可以用于概括序列并产生用于进一步处理的固定大小的表示。在结束处可能存在目标(如此处所示)，或者通过更下游模块的反向传播来获得输出$o^{(t)}$上的梯度。
现在我们研究图1中的RNN的前向传播公式。这个图没有指定隐藏单元激活函数。我们假设使用双曲正切激活函数。此外，图中没有明确指定何种形式的输出和损失函数。我们假定输出是离散的，如用于预测词或字符的RNN。表示离散变量的常规方式是把输出$o$作为每个离散变量可能值的非标准化对数概率。然后，我们可以应用softmax函数后续处理还有，获得标准化概率的输出向量$\hat{y}$。RNN从特定的初始状态$h^{0}$开始前向传播。从$t=1$到$t=\tau $的每个时间步，我们应用以下更新方程：
\(\begin{align}\alpha^{t}&=b+\omega h^{(t-1)}+Ux^{(t)} \\h^{(t)}&=\tanh(\alpha^{(t)}) \\o^{(t)}&=c+Vh^{t} \\ \hat{g}^{(t)}&=softmax(o^{(t)}) \end{align}\)
其中的参数的偏置$b$和$c$连同权重矩阵$U,V$和$W$,分别对应于输入到隐藏、隐藏到输出和隐藏到隐藏的连接。这个循环网络将一个输入序列映射到相同长度的输出序列。与$x$序列配对的$y$的总损失就是所有时间步的损失之和。例如，$L^{(t)}$为给定的$x^{(1)},····x^{(t)}$后$y^{(t)}$的负对数似然，则
\(\begin{align} &L({x^{(1)},···,x^{(\tau)}}),{y^{(1)},···,y……{(\tau)}} \\&=\sum L^{(t)}\\&=- \sum log p_{model}(y^{(t)} \mid {x^{(1)},····，x^{(t)}})\end{align}\)
其中$ p_{model}(y^{(t)} \mid {x^{(1)},····，x^{(t)}})$需要读取模型输出向量$\hat y^{(t)}$中对应于$y^{(t)}$的项。关于各个参数计算这个损失函数的梯度是计算成本很高的操作。梯度计算设计执行一次前向传播（如在图1 展开图中从左到右的传播），接着是由右到左的反向传播。运行时间$O(\tau)$。并且不能通过并行化来降低，因为前向传播图是固有循序的；每个时间步只能一前一后地计算。前向传播中各个状态必须保存，直到他们反向传播中被再次使用，因此内存代价也是$O(\tau)$。应用于展开图且代价为$O(\tau)$的反向传播算法称为通过时间反向传播(back-propagation through time,BPTT)。因此隐藏单元之间存在循环的网络非常强大但训练代价也很大。
导师驱动过程和输出循环网络
仅在一个事件步的输出和下一个时间步的隐藏单元间存在循环连接的网络(图2)确实没有那么强大(因为缺乏隐藏带隐藏的循环连接)。例如，它不能模拟通用图灵机。因为这个网络缺少隐藏到隐藏的循环，它要求输出单元捕捉用于预测未来的关于过去的所有信息。因为输出单元明确地训练成匹配训练集的目标，它们不太能捕获关于过去输入历史的必要信息，除非用户知道如何描述系统的全部状态，并将它作为训练目标的一部分。消除隐藏到隐藏循环的优点在于，任何基于比较时刻t的预测和时刻t的训练目标的损失函数的所有时间步都解耦了。因此训练可以并行化，即在各时刻t分别计算梯度。因为训练集提供输出的理想值，所有没必要先计算前一时刻的输出。
由输出反馈到模型产生循环连接的模型可用导师驱动过程进行训练。训练模型时，导师驱动过程不再使用最大似然准则，而在时刻$t+1$接收真实值$y^{(t)}$作为输入。我们可以通过检查两个时间步的序列得知这一点。条件最大似然准则是
\(\begin{align} &logp(y^{(1)},y^{(2)}\mid x^{(1)},x^{(2)})) \\& =logp(y^{(2)}\mid y^{(1)},x^{(2)})+ logp(y^{(1)}\mid x^{(1)},x^{(2)})\end{align}\)
在这个例子中，同时给定迄今为止的$x$序列和来自训练集的前一$y$值，我们可以看到在时刻$t=2$时，模型被训练为最大化$y^{(2)}$的条件概率。因此最大似然在训练时指定正确反馈，而不是将自己的输出反馈到模型。如下图所示
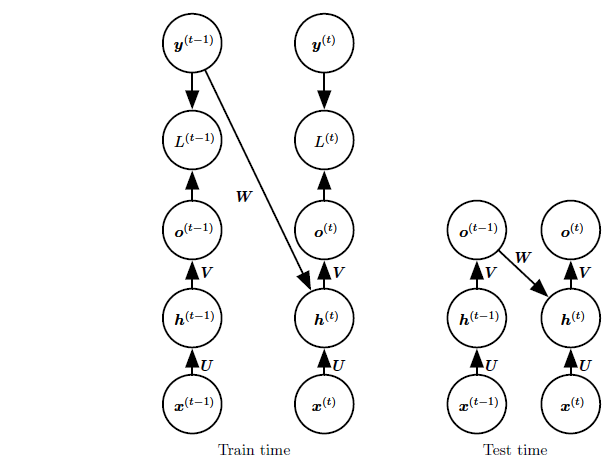
图示，导师驱动过程的示意图。导师驱动训练过程是一种训练技术，适用于输出与下一时间步的隐藏状态存在连接的RNN。(左)训练时，我们将训练集中正确的输出$y^{(t)}$反馈到$h^{(t+1)}$。(右)当模型部署后，真正的输出通常是未知的。在这种情况下，我们用模型的输出$O^{(t)}$近似正确的输出$y^{(t)}$，并反馈回模型。
作为有向图模型的循环网络
当我们使用一个预测性对数似然的训练目标，我们将RNN训练为能够根据之前的输入估计下一个序列元素$y^{(t)}$的条件分布。这可能意味着，我们最大化对数似然
\(log p(y^{(t)}\mid x^{(1)},···x^{(t)})\)
或者，如果模型包括来自一个时间步的输出到下一个时间步的连接，
\(log(y^{(t)}\mid x^{(1)},···,x^{(t)},y^{(1)},···,y^{(t-1)})\)
将整个序列$y$的联合分布分解为一系列单步的概率预测是捕获关于整个序列完整联合分布的一种方法。当我们不把过去的$y$值反馈给下一步作为预测的条件时，那么有向图模型不包含任何从过去$y^{(i)}$到当前$y^{(t)}$的边。在这种情况下，输出$y$与给定的$x$序列时条件独立的。当我们反馈真实的$y$值(不是它们的预测值，而是真正观测到或生成的值)给网络时，那么有向图模型包含所有从过去$y^{(i)}$到当前$y^{(t)}$的边
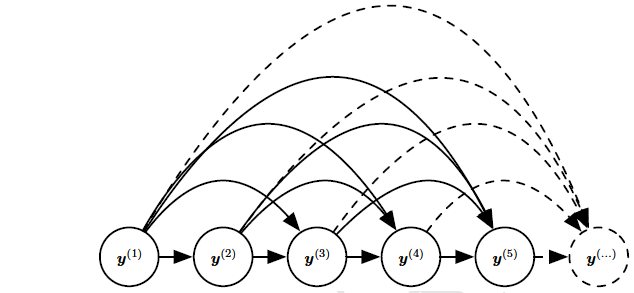
上图，序列$y^{(1)},···,y^{(t)}··,···$的全连接图模型。给定先前的值$y^{i}$可以影响一些$y^{(t)}(t \gt i)$的条件分布。当序列中的每个元素的输入和参数的数目越来越多，根据此图直接参数化图模型可能是非常低效的。RNN可以通过高效的参数化获得相同的全连接。如下图所示
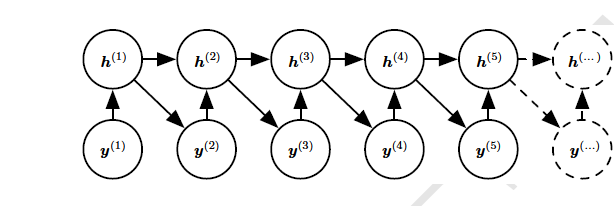
上图中：在RNN图模型中引入状态变量，尽管它是输入的确定性参数，但有助于我们根据关系式获得非常高效的参数化。序列中的每个阶段(对于$h^{(t)}和y^{(t)}$)使用相同的结构(每个节点具有相同数量的输入)，并且可以与其他阶段共享相同的参数。
基于上下文的RNN序列建模
上一节描述了没有输入x时，关于随机变量序列$y^{(t)}$的序列如何对应于有向图模型。一般情况下，RNN允许将图模型的观点扩展到不仅代表$y$变量的联合分布也能表示给定$x$后$y$条件分布。之前，我们已经讨论了将$t=1,···,\tau$的向量$x^{(t)}$序列作为输入的RNN。另一种选择是只使用单个向量$x$作为输入。当$x$是一个固定大小的向量时，我们可以简单地将其看作产生$u$序列RNN的额外输入。将额外输入提供到RNN的一些常见方法是：
- 在每个时刻作为一个额外输入，或
- 作为初始状态$h^{(0)}$,或
- 结合两种方式。
第一个 也是常用的方式如下图A所示。输入$x$和每个隐藏单元向量$h^{(t)}$之间的相互作用是通过新引入的权重矩阵$R$参数化的，这是只包含$y$序列的模型所没有的。同意的乘积$x^{T}R$在每个时间步作为隐藏单元的一个额外输入。我们可以认为$x$的选择(确定$x^{T}R$值)，是有效地用于每个隐藏单元的一个新偏置参数。权重于输入保持独立。我们可以认为这种模型采用了非条件模型的$θ$,并将$\omega$代入$θ$,其中$\omega$内的偏置参数现在是输入的函数。
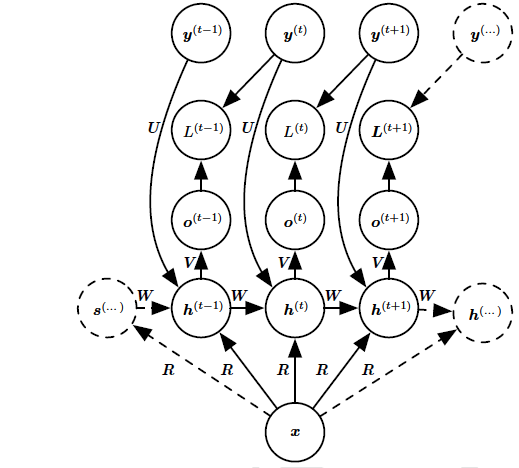
图A：将固定长度的向量$x$映射到序列$Y$上分布的RNN。这类RNN适用于很多任务如图注，其中单个图像作为模型的输入，然后产生描述图像的序列。观察到输出序列的每个元素$y^{(t)}$同时用作输入(对于当前时间步)和训练期间的目标(对于前一时间步)。
RNN可以接收向量序列$x^{t}$作为输入，而不是仅接收单个向量$x$作为输入。RNN对应的分布条件$P(y^{(1)},···,y^{(\tau)} \mid x^{(1)},···,x^)$,并在独立条件的假设下这个分布分解为
\(\Pi P(y^{(t)} \mid x^{(1)},···,x^{(t)})\)
为去掉条件独立的假设，我们可以在时刻$t$的输出到时刻$t+1$的隐藏单元添加连接，如下图B所示。该模型就可以代表关于$y$序列的任意概率分布。这种给定一个序列表示另一个序列分布的模型的还是有一个限制，就是这两个序列的长度必须是相同的。
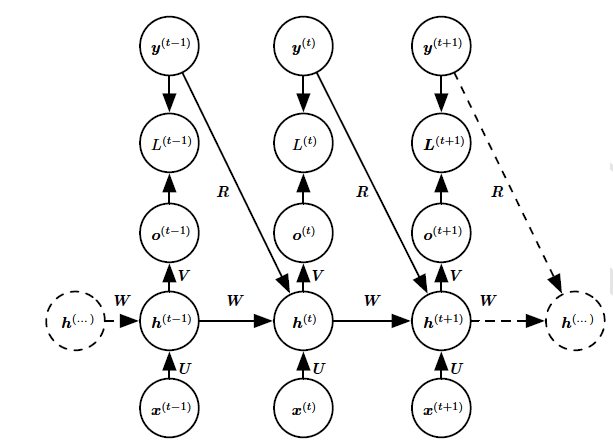图B:将可变长度的$x$值序列映射到相同长度的$y$值序列上分布的条件循环神经网络。图1，此RNN包含一个输出到当前状态的连接。这些连接允许此RNN对给定$x$的序列后相同长度的$y$序列上的任意分布建模。图1的RNN仅能表示在给定$x$值的情况下，$y$值彼此条件独立的分布。
参考
来源：deep learning,部分内容有删改
