双向RNN
目前为止我们考虑的所有循环神经网络有一个“因果”结构,意味着在时刻$t$的状态只能从过去的序列$x^{(1)},···x^{(x-1)}$以及当前的输入要$x^{(t)}$捕获信息。我们还讨论了某些在$y$可用时,允许过去的$y$值信息影响当前状态的模型。
然而,在许多应用中,我们要输出的$y^{(t)}$的预测可能依赖于整个输入序列。例如,在语音识别中,由于协同发音,当前声音作为音素的正确解释可能取决于未来几个音素,甚至潜在的可能取决于未来的几个词,因为词与附近的词之间的存在语义依赖:如果当前的词有两种声学上的合理解释,我们可能要在更远的未来(和过去)寻找信息区分它们。这在手写识别和许多其他序列到序列学习的任务中也是如此。
双向循环神经网络(或双向RNN)为满足这在需要而被发明。他们在需要双向信息的应用中非常成功,如手写识别,语音识别以及生物信息学。
顾名思义,双向RNN结合时间上从序列起点开始移动的RNN和另一个时间上从序列末尾开始移动的RNN。下图展示了典型的双向的RNN,其中$h^{(t)}$代表通过时间向前移动的子RNN状态,$g^{(t)}$代表通过时间向后移动的子RNN状态。这允许输出单元$O^{(t)}$能够计算同时依赖于过去和未来且对时刻$t$的输入值最敏感的表示,而不必指定$t$周围固定大小的窗口(这就是前馈网络、卷积网络或具有固定大小的先行缓存器的常规RNN所必须要做的)。
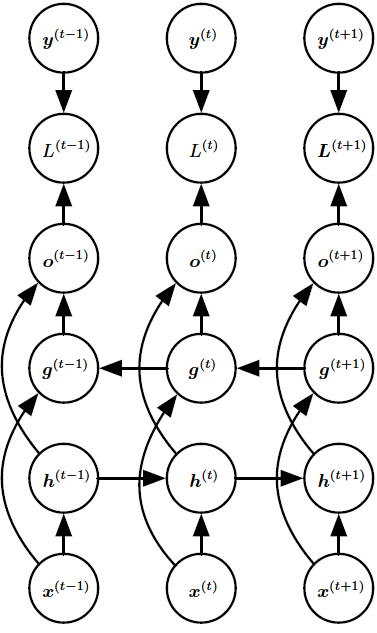
图1:典型的双向循环神经网络中的计算,意图学习将输入序列$x$映射到目标序列$y$(在每个步骤$t$具有损失$L^{(t)}$)。循环性$h$在时间上向前传播信息(向右),而循环性$g$在时间上向后传播信息(向左)。因此在每个点$t$,输出单元$O^{(t)}$可以受益于输入$h^{(t)}$中关于过去的相关概要以及输入$g^{(t)}$中关于未来的相关概要。
这个想法可以自然地扩展到2维输入,如图像,由四个RNN组成,每一个沿着四个方向中的一个计算:上、下、左、右。如果RNN能够学习到承载长期信息,那在2维网格每个点$(i,j)$的输出$O_{i,j}$就能计算一个能够捕捉到大多局部信息但仍依赖于长期输入的表示。相比卷积网络,应用于图像的RNN计算成本通常更高,但允许同一特征图的特征之间存在长期横向的相互作用。实际上,对于这样的RNN,前向传播公式可以写成表示使用卷积的形式,计算自底向上到每一层的输入(在整合横向相互作用的特征图的循环传播之前)。
基于编码-解码的序列到序列架构
本节我们讨论如何训练RNN,使其将输入序列映射到不一定等长的输出序列。这在许多场景中都有应用,如语音识别、机器翻译或回答,其中训练集的输入和输出序列的长度通常不相同(虽然它们的长度可能相关)。
用于映射可变长度序列到另一可变长度序列最简单的RNN架构最初由Choet al提出,之后不久由Sutskever et al(2014)独立开发,并且第一个使用这种方法获得翻译的最好结果。前一系统是对另一个机器翻译系统产生的建议进行评分,而后者使用独立的循环网络生成翻译。如下图2所示。这个想法非常简单:(1)编码器或读取器或输入RNN处理序列。编码器输出上下文$C$()通常是最终隐藏状态的简单函数)。(2)解码器或写入器或输出RNN则已固定长度的向量为条件产生输出序列$Y=(y^{(1)},····y^{(n_y)})$。编码器RNN的最后一个状态$h_{n_x}$通常被当作输入的表示$C$并作为解码器RNN的输入。
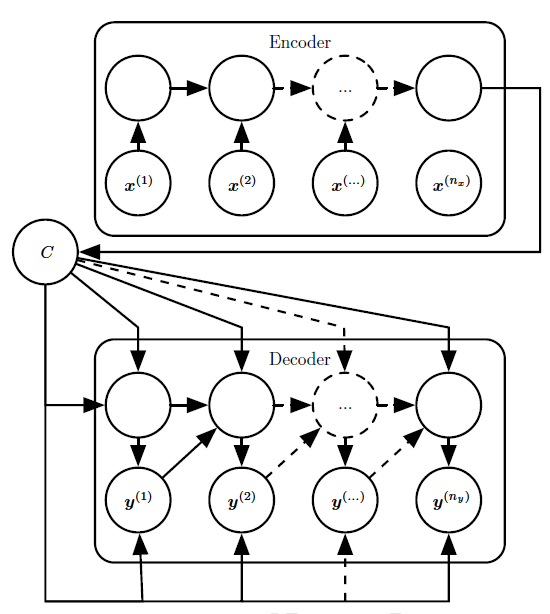
图2:在给定输入序列$(x^{(1)},x^{(2)}···,x^{(n_x)})$的情况下学习生成输出序列$(y^{(1)},y^{((2))},····y^{(n_y)})$的编码器-解码器或序列到序列的RNN架构的示例。它由读取输入序列的编码器RNN以及生成输出序列(或计算给定序列的概率)的解码器RNN组成。编码器RNN的最终隐藏状态用于计算一般固定大小的上下文变量$C$,$C$表示输入序列的语义概要并且作为解码器RNN输入。
如果上下文$C$是一个向量,则编码器RNN 只是向量到序列RNN。正如我们所见,向量到序列RNN至少有两种接收输入的方法。输入可以被提供为RNN的初始状态,或连接到每个时间步中的隐藏单元。这两种方式也可以结合。
深度循环网络
大多数RNN中的计算可以分解成三块参数及其相关的转换:
- 从输入到隐藏状态,
- 从前一隐藏状态到下一隐藏状态,以及
- 从隐藏状态到输出。
当网络被展开时,每个块对应一个浅的变换。能通过深度MLP内单个层表示的变换称为浅变换。通常,这是由学成的仿射变换和一个固定非线性表示组成的变换。
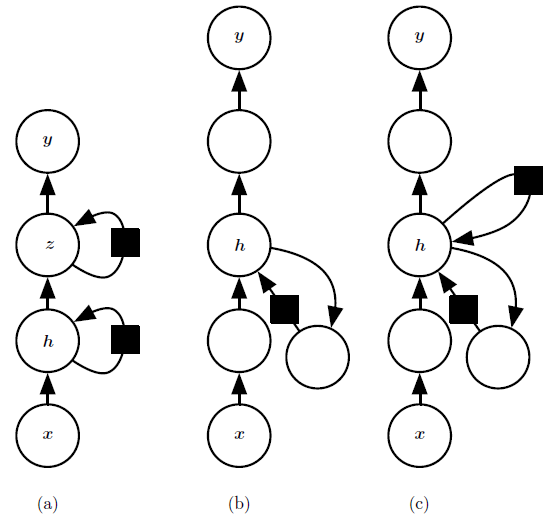
图3:循环神经网络可以通过许多方式变得更深。(a)隐藏循环状态可以被分解为具有层次的组。(b)可以向输入到隐藏,隐藏到隐藏以及隐藏到输出的部分引入更深的计算(如MLP).这可以延长链接不同的时间步的最短路径。(c)可以引入跳跃连接来缓解路径延长的效应。
递归神经网络
递归神经网络代表循环网络的另一个扩展,它被构造为深的树状结构而不是RNN的链状结构,因此是不同类型的计算图。递归网络的典型计算图如图4所示。递归神经网络由Pollack引入,而Bottou(2011)描述了这类网络的潜在用途-学习推论。递归网络已成功地应用于输入是数据结构的神经网络,如自然语言处理和计算机视觉。
递归网络的一个明显优势是,对于具有相同长度$\tau$的序列,深度(通过非线性操作的组合数量来衡量)可以急剧地从$\tau$减小为$O(log \tau)$,这可能有助于解决长期依赖。一个悬而未决的问题是如何以最佳的方式构造数。一种选择是使用不依赖于数据的树结构,如平衡二叉树。在某些应用领域,外部方法可以为选择适当的树结构提供借鉴。例如,处理自然语言的句子时用于递归网络的树结构可以被固定为句子语法分析树的结构(可以由自然语言语法分析程序提供)。理想情况下,人们希望学习器自行发现和推断适合于任意给定输入的树结构。
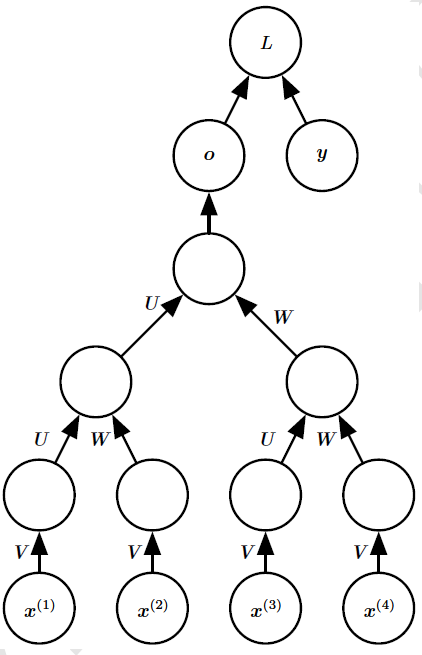
图4:递归网络将循环网络的链状计算图推广到树状计算图。可变大小的序列$x^{(1)},x^{(2)}···x^{(t)}$可以通过固定参数集合(权重矩阵$U,V,W$)映射到固定大小的表示(输出$o$)。该图展示了监督学习的情况,其中提供了一些与整个序列相关的目标$y$。
递归网络想法的 变种存在很多种。例如,Frasconi et al. (1997) 和Frasconi et al.(1998) 将数据与树结构相关联,并将输入和目标与树的单独节点相关联。由每个节点执行的计算无须是传统的人工神经计算(所有输入的仿射变换后跟一个单调非线性)。例如,Socher et al. (2013a) 提出用张量运算和双线性形式,在这之前人们已经发现当概念是由连续向量(嵌入)表示时,这种方式有利于建模概念之间的联系。
长短期记忆和其他门控RNN
实际应用中最有效的序列模型为门控RNN。包括长短期记忆和基于门控循环单元的网络。
像渗漏单元一样,门控RNN想法也是基于生成通过时间的路径,其中导数既不消失也不发生爆炸。渗漏单元通过手动选择常量的连接权重或参数化的连接权重来达到这一目的。门控RNN将其推广为每个时间步都可能改变的连接权重。
渗漏单元允许网络在较长持续时间内积累信息。然而,一旦该信息被使用,让神经网络遗忘旧的状态可能是有用的。例如,如果一个序列是由子序列组成,我们希望渗漏单元能在各子序列内积累线索,我们需要将状态设置为0以忘记旧状态的机制。我们希望神经网络学会决定何时清除状态,而不是手动决定。这就是门控RNN要做的事情。
LSTM
引入自循环的巧妙构思,以产生梯度长时间持续流动的路径是初始长短期记忆(LSTM)模型的核心贡献。其中一个关键扩展是使自循环的权重视上下文而定,而不是固定的。门控此自循环(由另一个隐藏单元控制)的权重,累计的事件尺度可以动态地改变。在这种情况下,即使是具有固定参数的$\text{LSTM}$,累积的时间尺度也可以因输入序列而改变,因为时间常数是模型本身的输出。
$\text{LSTM}$块如图5所示。
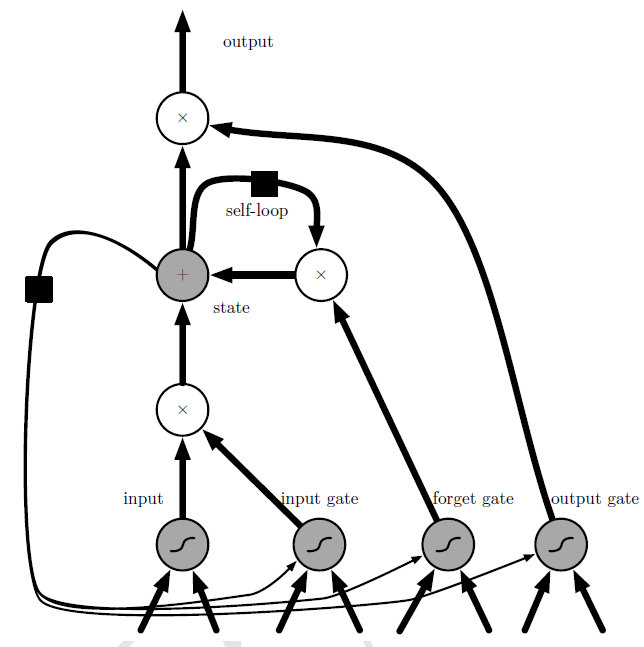
图5:$\text{LSTM}$循环神经网络的“细胞”的框图。细胞彼此循环连接,带她一般循环网络中普通的隐藏单元。这里使用常规的人工神经元计算输入特征。如果sigmoid输入门允许,它的值可以累加到状态。状态单元具有线性自循环,其权重由遗忘门控制。细胞的输出可以被输出门关闭。所有门控单元都有sigmoid非线性,而输入单元可具有任意的压缩非线性。状态单元也可以用作门控单元的额外输入。黑色方块表示单个时间步的延迟。
在浅循环网络的架构下,相应的前向传播公式如下。$\text{LSTM}$循环网络除了外部的RNN循环外,还具有内部的“$\text{LSTM}$细胞”循环(自环),因此$\text{LSTM}$不是简单地向输入和循环单元的仿射变换之后施加一个逐元素的非线性。与普通的循环网络类似,每个单元有相同的输入和输出,但也有更多的参数和控制信息流动的门控单元系统。最重要的组成部分是状态单元$s_{i}^{(t)}$。此处自环 的权重(或相关联的时间常数)由遗忘门$f_{i}^{(t)}$控制(时刻$t$和细胞$i$),you sigmoid单元将权重设置为0和1之间的值:
\(f_{i}^{(t)}=\sigma(b_{i}^{f}+\sum U_{(i,j)}^fx_{j}^{(t)}+\sum W_{i,j}^fh_{j}^{(t-1)})\)
其中$x^{(t)}$是当前输入向量,$h^{(t)}$是当前隐藏层的向量,$h^{(t)}$包含所有$\text{LSTM}$细胞的输出。$b^{f},U^{f},W^{f}$分别是偏置、输入权重和遗忘门的循环权重。因此$\text{LSTM}$细胞内部状态以如下方式更新,其中有一个条件的自环权重$f_{i}^{(t)}$:
\(s_{i}^{(t)}=f_{i}^{(t)}s_{i}^{(t-1)}+g_{i}^{(t)}\sigma (b_i+\sum U_{i,j}x_{j}^{(t)}+\sum W_{i,j}h_{j}^{(t-1)})\)
其中$b,U,W$分别是$\text{LSTM}$细胞中的偏置、输入权重和遗忘门的循环权重。外部输入门单元$g_{i}^{(t)}$以类似遗忘门(使用sigmoid获得一个0和1之间的值)的方式更新,但有自身的参数:
\(g_{i}^{(t)}=\sigma (b_{i}^{g}+\sum_{j} U_{i,j}^g)x_{j}^{(t)}+\sum_{j}W_{i,j}^gh_{j}^{(t-1)}\)
$\text{LSTM}$细胞的输出$h_{i}^{(t)}$也可以由输出门$q_{i}^{(t)}$关闭(使用sigmoid 单元作为门控):
\(\begin{align} h_{i}^{(t)}&=tanh(s_{i}^{(t)})q_{i}^{(t)} \\q_{i}^{(t)}&=\sigma(b_{i}^{o}+\sum_{j}U_{i,j}^{o}x_j^{(t)}+\sum_{j}W_{i,j}^{o}h_{j}^{(t-1)})\end{align}\)
其中$b^{o},U^{o},W^{o}$分别是偏置、输入权重和遗忘门的循环权重。在这些变体中,可以选择使用细胞状态$s_{i}^{(t)}$作为额外的输入(及其权重),输入到第$i$个单元的三个门,如图5所示。
$\text{LSTM}$网络比简单的循环架构更易于学习长期依赖,先是用于测试长期依赖学习能力的人工数据集,然后是在具有挑战性的序列处理任务上获得最先进的表现。
参考
来源:deep learning,部分内容有删改