概率论是用于表示不确定性声明的数学框架。它不仅提供了量化不确定性的方法,也提供了用于导出新的不确定性声明的公理。在人工智能领域,概率论主要由两种用途。首先,概率论告诉我们AI系统如何推理,据此我们设计一些算法来计算或者估算概率论导出的表达式。其次,我们可以用概率和统计从理论上分析我们提出的AI系统的行为。
1.为什么要使用概率论
计算机科学的许多分支处理的实体大部分都是完全确定且必然的。程序员通常可以安全地假定CPU将完美地执行每天机器指令。鉴于许多科学家和软件工程师在一个相对干净和确定的环境中工作,机器学习对于概率论的大量使用是很令人吃惊的。
这是因为机器学习通常处理不确定量,有是也可能需要处理随机(非确定性的)量。不确定性和随机性可能来自多个方面。至少从20世纪80年代开始,研究人员就对使用概率论来量化不确定性提出了令人信服的论据。
在很多情况下,使用一些简单而不确定的规则要比复杂而确定的规则更为实用,即使真正的规则是确定的并且我们建模的系统可以足够精确地容纳复杂的规则。例如,简单的规则“多数鸟儿都会飞”的描述很简单并且使用广泛,而正式的规则——“除了那些非常小的还没学会飞翔的幼鸟,因为生病或是受伤而失去了飞翔能力的鸟,不会飞的鸟类包括食火鸟、鸵鸟、几维……等等,鸟会飞”,很难应用、维护和沟通,即使经过所有这些的努力,这些规则还是很脆弱的,并且容易失效。
尽管我们的确需要一种用以对不确定性进行表示和推理的方法,但是概率论并不能明显地提供我们在人工智能领域需要的所有工具。概率论最初的发展是为了分析事件发生的频率。我们可以很容易地看出概率论,对于像在扑克牌游戏中抽出一手特定的牌这种事件的研究中,是如何使用的。这类事件往往是可以重复的。当我们说一个结果发生的概率为$p$,就意味着如果我们反复实验(例如,抽取一手牌)无限次,有$p$的比例会导致这样的结果。这种推理似乎并不立即适用于那些不可重复的命题。如果一个医生诊断了病人,并说病人患流感的几率为40%,这意味着非常不然的事情——我们既不能让病人有无穷多的副本,也没有任何理由去相信病人的不同副本在具有不同的潜在条件下表现出相同的症状。在医生诊断病人的情况下,我们用概率来表示一种信任度(degree of belief),其中1表示非常肯定病人患有流感,而0表示非常肯定病人没有流感。前面一种概率,直接与事件发生的频率相联系,被称为频率派概率(frequentist probability);而后者,设计到确定性水平,被称为贝叶斯概率(Bayesian probability)。
概率可以被看做是用于处理不确定性的逻辑扩展。逻辑提供了一套形式化的规则,可以在给定某些命题是真是假的假设下,判断另外一些命题是真的还是假的。概率论提供了一套形式化的规则,可以在给定一些命题的似然后,计算其他命题为真的似然。
2.随机变量
随机变量(random variable)是可以随机地取不同值的变量。我们通常用无格式字体中的小写字母来表示随机变量本身,而用手写体中的小写字母来表示随机变量能够取到的值。例如,$x_1$和$x_2$都是随机变量$\mathbb{x}$可能的取值。对于向量值变量,我们会将随机变量写成$X$,它的一个可能取值为$x$。就其本身而言,一个随机变量只是对可能状态的描述;它必须伴随着一个概率分布来指定每个状态的可能性。
随机变量可以是离散的或者连续的。离散随机变量拥有有限或者可数无限多的状态。注意这些状态不一定非要是整数;它们也可能只是一些被命名状态而没有数值。连续随机变量伴随着实值。
3.概率分布
概率分布(probability distribution)是用来描述随机变量或一簇随机变量在每一个可能取到的状态的可能性大小。我们描述概率分布的方式取决于随机变量是离散的还是连续的。
3.1离散型变量和概率质量函数
离散型变量的概率分布可以用概率质量函数(probability mass function,PMF)来描述。我们通常用大写字母$P$来表示概率质量函数。通常每一个随机变量都会有一个不同的概率质量函数,并且读者必须根据随机变量来推断所使用的PMF,而不是根据函数的名词来推断;例如,$P(x)$通常和$p(y)$不一样。
概率质量函数将随机变量能够取得的每个状态映射到随机变量取得该状态的概率。$\mathbb {x}=x$的概率用$P(x)$来表示,概率为1表示$\mathbb{x}=x$是确定的,概率为0表示$\mathbb {x}=x$是不可能发生的。
概率质量函数可以同时作用于多个随机变量。这种多个变量的概率分布被称为联合概率分布(joint probability distribution)。$P(\mathbb{x}=x,\mathbb{y}=y)$表示$\mathbb{x}=x$和$\mathbb{y}=y$同时发生的概率。我们也可以简写为$P(x,y)$。
如果一个函数$P$是随机变量$\mathbb{x}$的PMF,必须满足下面这几个条件:
- $P$的定义域必须是$\mathbb{x}$所有状态的集合。
- $\forall x \in \mathbb{x}, 0 \leq P(x) \leq1.$不可能发生的事件概率为0,并且不存在比这概率更低的状态。类似的,能够确保一定发生的事件概率为1,而且不存在比这概率更高的状态。
- $\sum_{x \in \mathbb{x}}=1$.我们把这条性质称之为归一化的。如果没有这条性质,当我们计算很多事件其中之一发生的概率可能会得到大于1的概率。
3.2连续型变量和概率密度函数
当我们研究的对象是连续型随机变量时,我们用概率密度函数(probability density function PDF)而不是概率质量函数来描述它的概率分布。如果一个函数$p$是概率密度函数,必须满足下面这几个条件:
- $p$的定义域必须是$\mathbb{x}$所有可能状态的集合。
- $\forall x \in \mathbb{x},p(x) \ge0$.注意,我们并不要求$p(x)\leq1$。
- $\int P(x)dx=1$
概率密度函数$p(x)$并没有直接对特定的状态给出概率,相应的,它给出了落在面积为$\delta x$的无限小的区域内的概率为$p(x) \delta x$。
我们可以对概率密度函数求积分来获得点集的真实概率质量。特别地,$x$落在集合$S$中的概率可以通过$p(x)$对这个集合求积分来得到。在单变量的例子中,$x$落在区间$[a,b]$的概率是$\int _{[a,b]}p(x)dx$。
4.边缘概率
有时候,我们知道了一组变量的联合概率分布,但想要了解其中一个子集的概率分布。这种定义在子集上的概率分布被称为边缘概率分布(marginal probability distribution)。
例如,假设有离散型随机变量$\mathbb{x}$和$\mathbb{y}$,并且我们知道$P(\mathbb{x,y})$。我们可以根据下面的求和法则来计算$P(\mathbb{x})$:
\[\forall x \in \mathbb{x},P(\mathbb{x}=x)=\sum_y P( \mathbb{x}=x,\mathbb{y}=y) \quad 式(1)\]“边缘概率”的名称来源于手算边缘概率的计算过程、当$P(\mathbb{x,y})$的每个值被写在由每行表述不同的$x$值,每列表示不同的$y$值形成的网格中时,对网格中的每行求和是很自然的事情,然后将求和的结果$P(x)$写在每行右边的纸的边缘处。
对应连续型变量,我们需要用积分替代求和:
\[P(x)=\int p(x,y)dy\quad 式(2)\]5.条件概率
在很多情况下,我们感兴趣的是某个事件,在给定其他事件发生时出现的概率。这种概率叫做条件概率。我们将给定$\mathbb{x}=x,\mathbb{y}=y$发生的条件概率记为$P(\mathbb{y}=y \mid \mathbb{x}=x)$。这个条件概率可以通过下面的公式计算:
\[P(\mathbb{y}=y \mid \mathbb{x}=x)= \frac {P( \mathbb{y}=y,\mathbb{x}=x)} {P(\mathbb{x}=x)} \quad 式(3)\]条件概率只在$P(\mathbb{x}=x) > 0$时有定义。我们不能计算给定在永远不会发生的事件上的条件概率。
这里需要注意的是,不要把条件概率和计算当采用某个动作后会发生什么相混淆。假定某个人说德语,那么他是德国人的条件概率是非常高的,但是如果随机选择的一个人会说德语,他的国籍不会因此改变。计算一个行动的后果被称为敢于查询。
6.条件概率的链式法则
任何多维随机变量的联合概率分布,都可以分解成只有一个变量的条件概率相乘的形式:
\[P(\mathbb{x^{(1)}},...,\mathbb{x^{(n)}})=P(\mathbb{x^{(1)}} \Pi(\mathbb{x^{(i)}}\mid \mathbb{x^{(1)}},...,\mathbb{x^{(i-1)}}))\quad 式(4)\]这个规则被称为概率的链式法则(chain rule)或者乘法法则(product rule)。他可以直接从式(3)条件概率的定义得到。例如,使用两次定义可以得到
\[\begin{align} P(a,b,c)&=P(a\mid b , c)P(b,c) \\ P(b,c)&=P(b\mid c)P(c)\\ P(a,b,c)&=P(a\mid b,c)P(b\mid c)P(c)\end{align}\]7.独立性和条件独立性
两个随机变量$\mathbb{x}$和$\mathbb{y}$,如果它们的概率分布可以表示成两个因子的乘积形式,并且一个因子只含$\mathbb{x}$另一个因子只包含$\mathbb{y}$,我们就称两个随机变量是相互独立的:
\[\forall x \in \mathbb{x},y \in \mathbb{y},p(\mathbb{x}=x,\mathbb{y}=y)=p(\mathbb{x}=x)P(\mathbb{y}=y)\quad 式(5)\]如果关于$\mathbb{x}$和$\mathbb{y}$的条件概率分布对于$z$的每一个值都可以写成乘积的形式,那么这两个随机变量$\mathbb{x}$和$\mathbb{y}$在给定随机变量$z$时是条件独立的: \(\forall x \in \mathbb{x} ,y \in \mathbb{y},z \in \mathbb{z}, p(\mathbb{x}=x,\mathbb{y}=y \mid \mathbb{z}=z)=p(\mathbb{x}=x\mid \mathbb{z}=z)p(\mathbb{y}=y\mid \mathbb{z}=z) \quad 式(6)\)
我们可以采用一种简化形式来表示独立性和条件独立性:$\mathbb{x} \perp \mathbb{y}$表示$\mathbb{x}$和$\mathbb{y}$相互独立,$\mathbb{x} \perp \mathbb{y} \mid \mathbb{z}$表示$\mathbb{x}$和$\mathbb{y}$在给定$\mathbb{z}$时条件独立。
8.期望、方差和协方差
函数$f(x)$关于某分布$P(x)$的期望(expectation)或者期望值(expectation value)是指,当$x$由$P$产生,$f$作用于$x$时,$f(x)$的平均值。对于离散型随机变量,这可以通过求和得到:
\[E_{x\sim P}[f(x)]=\sum_xP(x)f(x) \quad 式(7)\]对于连续型随机变量可以通过求积分得到:
\[E_{x \sim p}[f(x)]=\int p(x)f(x)dx \quad 式(8)\]当概率分布在上下文中指明时,我们可以只写出期望作用的随机变量的名词来进行简化,例如$E_x[f(x)]$。如果期望作用的随机变量也很明确,我们可以完全不写脚标,就像$E[f(x)]$。
方差(variance)衡量的是当我们对$x$依据它的概率分布进行采样时,随机变量$x$的函数值会呈现多大的差异:
\[Var(f(x))=E[(f(x)-E[f(x)])^2] \quad 式(9)\]当方差很小时,$f(x)$的值形成的簇比较接近它们的期望值。方差的平方根被称为标准差(standard deviation)。
协方差(covariance)在某种意义上给出了两个变量线性相关性的强度以及这些变量的瓷都:
\[Cov(f(x),g(y))=E[(f(x)-E[f(x)])(g(y)-E[g(y)])]\quad 式(10)\]协方差的绝对值如果很大则意味着变量值变化很大并且它们同时距离各自的均值很远。如果协方差是正的,那么两个变量都倾向于同时取得相对较大的值。如果协方差是负的,那么其中一个变量倾向于取得相对较大的值的同时,另一个变量倾向于取得相对较小的值,反之亦然。其他的衡量指标如相关系数(correlation)将每个变量的贡献归一化,为了衡量变量的相关性而不受各个变量尺度大小的影响。
协方差和相关性是有联系的,但实际上不同的概念。它们是有联系的,因为两个变量如果相互独立那么它们的协方差为零,如果两个变量的协方差不为零那么它们一定是相关的。然而,独立性又是和协方差完全不同的性质。两个变量如果协方差为零,它们之间一定没有线性关系。独立性是比零协方差的要求更强,因为独立性还排除了非线性的关系。两个变量相互依赖但是具有零协方差是可能的。例如,假设我们首先从区间[-1,1]上的均匀分布中采样出一个实数$x$。然后我们对一个随机变量$s$进行采样。$s$以$ \frac{1}2$的概率值为1,否则为-1.我们可以通过令$y=sx$来生成一个随机变量$y$。显然$x$和$y$不是相互独立的,因为$x$完全决定了$y$的尺度。然而,$Cov(x,y)=0$。
9.高斯分布
实数上最常用的分布就是正态分布(normal distribution),也称为高斯分布(Gaussian distribution):
\[Ñ(x;\mu,\delta^2)= \sqrt{\frac{1}{2\pi\delta^2}}exp \big(-\frac{1}{2\delta^2}(x-\mu)^2\big) \quad 式(11)\]下图画出了正态分布的概率密度函数
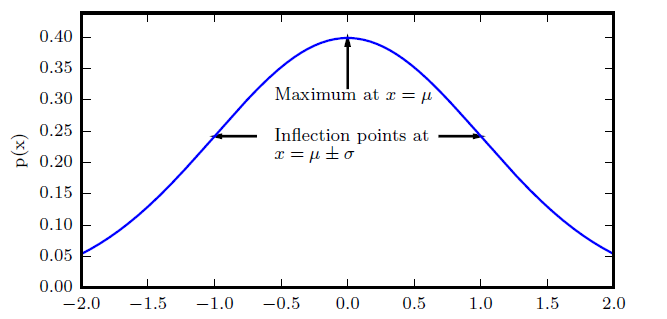
图示:正态分布。正态分布$Ñ(x;\mu,\delta^2)$呈现经典的“钟型曲线”的性质,其中中心峰的$x$坐标有$\mu$给出,峰的宽度受$\delta$控制。在这个示例中,我们展示的是标准正态分布,其中$\mu=0.\delta=1$。
采用正态分布在很多应用中都是一个明智的选择。当我们由于缺乏关于某个实数上分布的先验只是而不知道该选择怎样的形式时,正态分布是默认的比较好的选择,其中两个原因。
第一,我们想要建模的很多分布的真实情况是比较接近正态分布的。中心极限定理(central limit theorem)说明很多独立随机变量的和近似服从正态分布。这意味着在实际中,很多复杂系统都可以被成功地建模成正态分布的噪声,即使系统可被分解成一些更结构化的部分。
第二,在具有相同方差的所有可能的概率分布中,正态分布在实数上具有最大的不确定性。因此,我们可以认为正态分布是对模型加入的先验只是量最少的分布。充分利用和证明这个想法需要更多的数学工具。
正态分布可以推广到$R^n$空间,这种情况下被称为多维正态分布(multivariate normal distribution)。它的参数是一个正定对称矩阵$\sum$: \(Ñ(x;\mu,\sum)=\sqrt{\frac{1}{(2\pi)^2det(\sum)}}exp\big(-\frac{1}{2}(x-\mu)^T\sum^{-1}(x-\mu)\big)\quad 式(12)\)
参数$\mu$仍然表示分布的均值,只不过现在是向量值。参数$\sum$给出了分布的协方差矩阵。和单变量的情况类似,当我们希望对很多不同参数下的概率密度函数多次求值时,协方差矩阵并不是一个很高效的参数化分布的方式,因为对概率密度函数求值时需要对$\sum$求逆。我们可以使用一个精度矩阵(precision matrix)$\beta$进行替代:
\[Ñ(x;\mu,\beta^{-1})=\sqrt{\frac{det(\beta)}{(2\pi)^n}}exp\big(-\frac{1}{2}(x-\mu)^T\beta(x-\mu)\big)\quad 式(13)\]我们常常把协方差矩阵固定成一个对角阵。一个更简单的版本是各向同性(isotropic)高斯分布,它的协方差矩阵是一个标量乘以单位阵。
参考
来源:deep learning,部分内容有删改