事件抽取是自然语言处理中一个重要任务。在现实世界中,一个句子中会经常出现多个事件,抽取单一事件要比抽取多个事件要简单的多。常见的事件抽取方法是通过对句子顺序建模建立起多个事件之间的关联关系,这种方法在捕获长远距离的依赖关系会受到非常大的影响。本文是发表在EMNLP 2018上的一篇关于事件抽取的联合模型论文,主要介绍了一种引入句法分析信息和图卷积网络来编码图信息,同时抽取触发词和论元。在ACE 2005的英文数据集上取得了与目前最先进系统相当的性能。
任务介绍
事件抽取有两个子任务,分别是触发词抽取和论元抽取。具体来说就是,给一个句子或一个段落,事件抽取系统需要识别出事件触发词并判别出触发词的类别,以及对应论元的角色。
举个例子,在下面句子中,
“He left the company, and planned to go home directly”。
触发词”left“可能触发了”Transport“(运输)事件,或者”End-Position“(离职)事件。然而,如果我们考虑了接下来的触发词”go“,就更确定的判断”left“触发的事件是”Transport“,就像”Injure“(受伤)事件和”Die“(死亡)事件经常出现在一起。本文认为这种现象在现实世界中很常见。文中提出对句子按照顺序进行序列编码,对于捕获句子的长远距离依赖关系是非常低效的。另外这些模型不能充分的捕获事件之间的联系。为了解决这个问题,本文提出引入语言学的依存句法分析中的短弧来引导信息从一个点流入目标点中。与顺序序列编码相比较,对这些弧进行编码能够成功的减少从一个事件触发词跳跃到另一个触发词需要的步数。我们来看下面的一个例子。
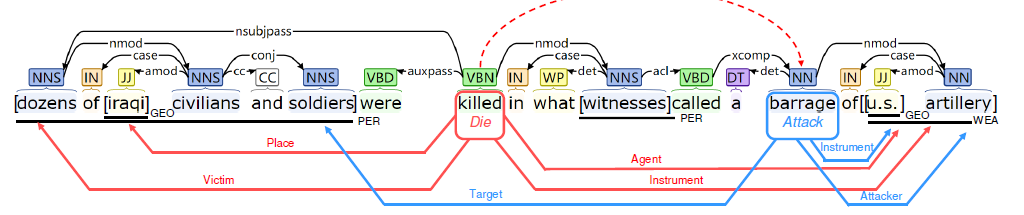
图中句子中有两个事件,”killed“触发了”Die“事件,还有四个论元(红色标记),”barrage“触发了”Attack“事件,有三个论元(蓝色标记)。顺序编码,从”killed“到”barrage“需要六步,如果根据依存句法树中的弧(沿着nmod弧从”killed“到”witness“,然后沿着”acl“弧从”witness“到”called“,最后沿着”xcomp“弧从called到”barrage”)。这三条弧包含了一条短路径,引导着依存句法信息流从”killed“到”barrage“。
模型
本文提出了一个Joint Multiple Events Extraction(JMEE)模型,通过引入句法短弧来增强信息流动和基于注意力机制的图卷积网络来编码图信息。图卷积(graph convolutional networks)能够学习图中邻近节点的每个节点的语法上下文表示。在这里我们主要关注图卷积网络(GCN)模型。
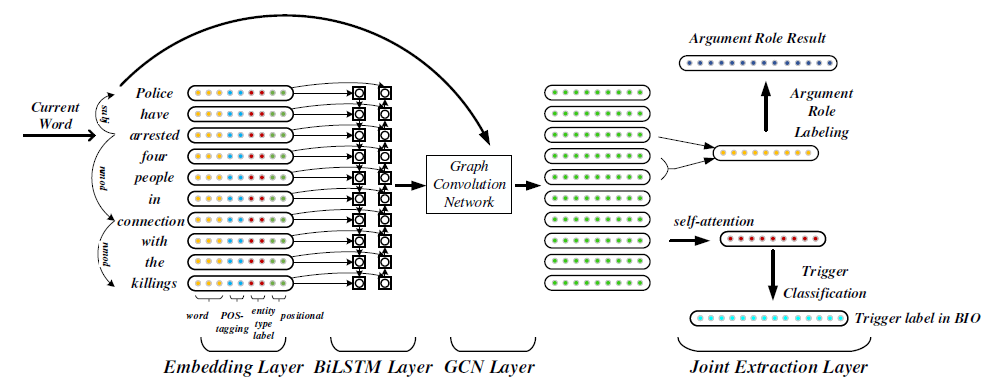
模型主要包含四个部分,(1):句子表示部分,文中使用词向量表示一个句子;(2)图卷积网络对依存图中的弧执行卷积操作;(3)对触发词使用自注意力机制,将句子中多个事件联系在一起;(4)论元分类,对每个候选实体进行角色分配。
从图中可以看到,文章使用了词性标注(pos)特征、实体(entity)特征以及触发词位置特征,将这些特征向量化得到实值向量与句子向量拼接在一起得到输入$X$,然后将$X$送入到Bi-LSTM和GCN中学习到更有效的表示。
图卷积网络
对句子进行依存句法分析,得到一个无向图$\mathcal{G}=(\mathcal{V},\varepsilon)$,其中$\mathcal{V}=v_1,v_2,…v_n(\mid \mathcal{V}\mid=n)$,$\varepsilon$是边和节点的集合。在$\mathcal{V}$中,$v_i$是句子$W$中的第$i$个词的边。边$(v_i,v_j) \in {\epsilon}$表示节点$v_i$直接到$v_j$的弧,标签$K(w_i,w_j)$,另外,为了使信息沿着反方向流动,我们将弧反转成$(v_j,v_i)$,标签为$K^{‘}(w_i,w_j)$,文中还增加了“自循环”,例如$(v_i,v_i)$。
因此,在第$h$层的句法图卷积层中,对于节点$v$,我们能够通过以下公式计算图卷积向量$h_v^{k+1}$
\[h_v^{(k+1)}=f(\sum_{u\in \mathcal{N}(v)}(W^{(K)}_{K(u,v)}h_{u}^{(k)}+b^{k}_{K(u,v)}))\]其中$K(u,v)$是边$(u,v)$边的标签,$ W^{(k)}_{K(u,v)}$ 和 $ b_{K(u,v)}^{(k)} $ 分别是类别$K(u,v)$的权重矩阵和偏置;$ \mathcal{N(v)}$ 是包括$u$在内的邻近节点;$f$是激活函数。此外,文中使用 $x_i$ 的词向量初始化GCN的第一层节点 $h_{vi}^0$。
假设弧的标签数量有$N$个,按照上述公式会将标签数量翻倍。这意味着一层GCN,我们就会有$2N+1$的参数对。本文使用的斯坦福句法分析,大概有50种依存句法关系,为了减少参数,修改标签$K(w_i,w_j)$为
\[K(w_i,w_j) = \left\{ \begin{array}{ll} along & \textrm(v_i,v_j)\in \epsilon\\ rev & \textrm i!=j\&{(v_j,v_i)\in \epsilon}\\ loop & \textrm{i==j} \end{array} \right.\]但是,不是所有类型的边都能对下游任务进行信息传递,因为在生成依存句法树时依然会产生噪声,所以我们在边上使用门来控制它们的重要性。
\[g^{(k)}{u,v}= \sigma(h_u^{(k)}V{K{(u,v)}^{(k)}}+d^{(k)}{(u,v)})\]其中$\sigma$是逻辑斯特回归函数,$V_{K(u,v)}^{(k)}$和$d_{K(u,v)}^{(k)}$是门的权重矩阵和偏置。使用了额外的门控机制,最后的GCN计算如下
\[h_{v}^{(k+1)}=f(\sum_{u\in\mathcal{N}}g^{(k)}_{K(u,v)}(W_{K(u,v)}^{(k)}h_u^{(k)}+b^{(k)}_{K(u,v)})\]由于堆叠$k$层GCN能够模拟$k$步的信息,有时两个触发词之间的跳跃长度小于$k$,为了避免信息过渡传播,我们采用了高速公路,允许信息无障碍的流过堆叠的GCN层。高速公路层进行非线性变换如下
\[t=\sigma(W_Th^{k}_v+b_T)\] \[\overline{h}^{(k+1)}_v=h^{(k+1)}_v+t \odot g(W_Hh^k_v+b_H)+(1-t)\odot h^k_v\]因此,第$k$层GCN输入应该是$\overline{h}^{(k)}$而不是$h^{(k)}$。
图卷积网络能够捕获弧之间的依赖关系,但GCN的数量限制了图卷积捕获信息的能力。然而,我们发现在不增加GCN层数的情况下,利用局部序列信息将会扩大信息流,所以Bi-LSTM和GCN是互补,互相促进的。因此,我们不直接将句子向量$X$输入到图卷积层中,而是首先将$X$输入到Bi-LSTM中去,编码句子得到新的表示,
\[\overrightarrow{p}_t=\overrightarrow{LSTM}(\overrightarrow{p}_{t-1},x_t)\] \[\overleftarrow{p}_t=\overleftarrow{LSTM}(\overleftarrow{p}_{t-1},x_t)\]输入到GCN层中的是$\overline{x}_t=[\overrightarrow{p}_t,\overleftarrow{p}_t]$,其中”,”是个连接操作。Bi-LSTM自适应的累积和抽象句子中每个词的上下文表示。
实验结果
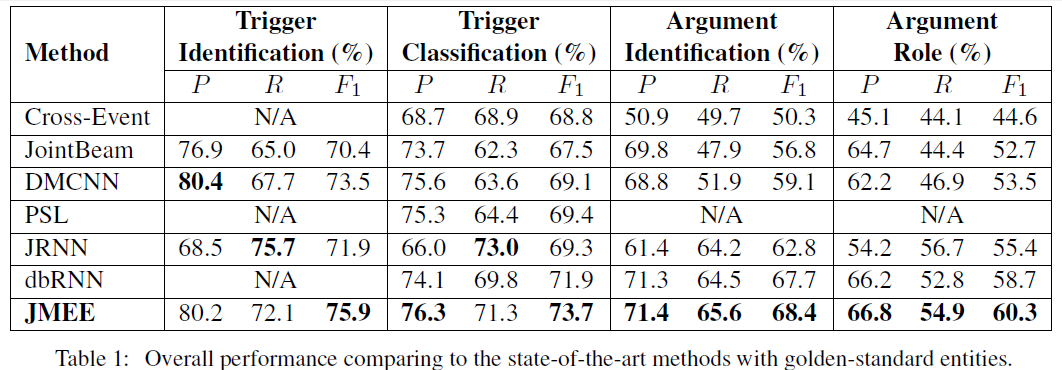
作者在ACE 2005的英文数据集上做实验测试得出结论,该文中提出的联合方法效果最佳。实验结果如下所示,表明提出的方法能够有效的联合图卷积和句法路径,并且在抽取句子中多事件的效果尤佳。