本篇博文主要介绍beam search(束搜索)的基本原理以及其高效的实现方式。beam search广泛的应用在seq2seq模型中。但我尚未掌握其中的细节,目前为止,openNMT-py 是我见过最强大的翻译器和预测器,拥有着数量巨大的参数和广泛选项。
写这篇文章要比想象中难得很多。我发现很难简单一边介绍流程的内部工作原理,一边还要覆盖重要的代码块。由于这一困难,这篇博客被分成两部分,一个基础教程和一个高级教程,以免造成太多干扰。
写完这篇博文后,我对beam search知识的理解非常自信,希望你阅读后也有同样的感觉。
本篇博文主要翻译于Implementing Beam Search — Part 1
Seq2Seq和Beam Search框架
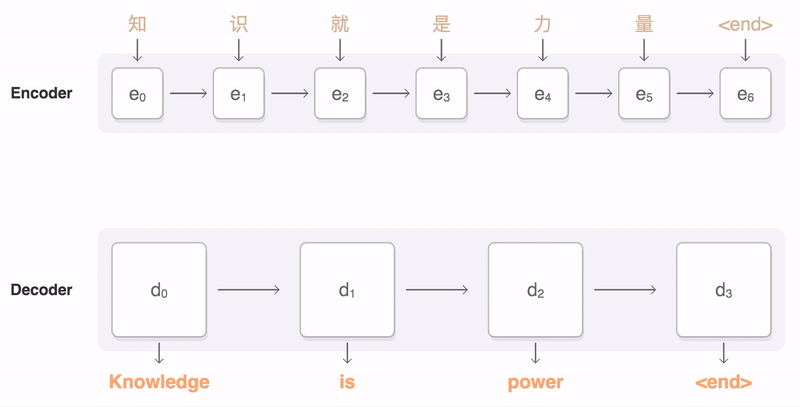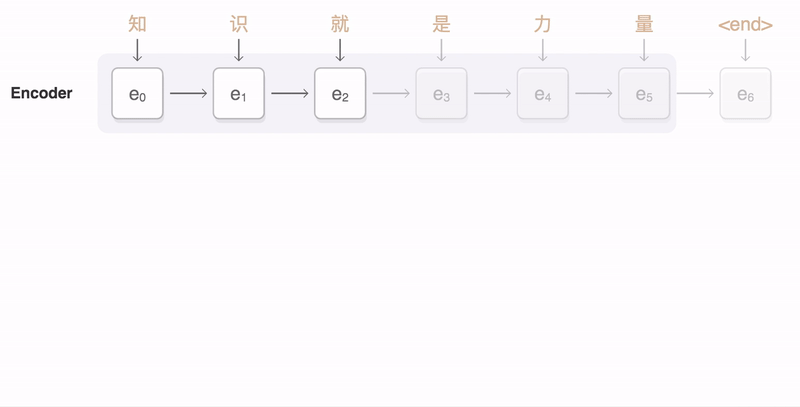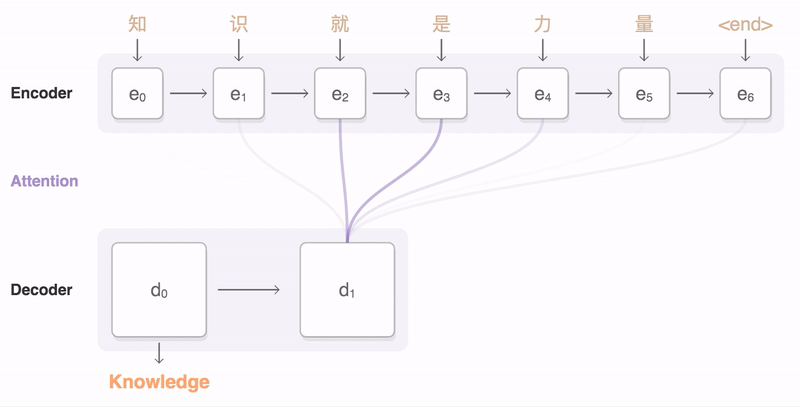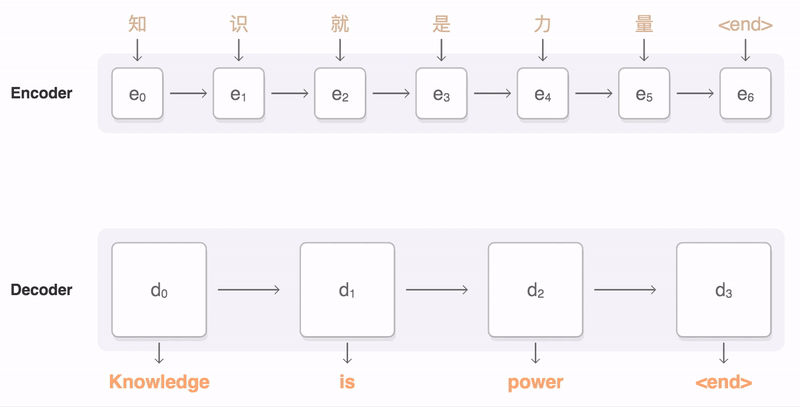
seq2seq(Sequence-to-Sequence)模型将一个输入序列映射到输出序列。输入序列被送到编码器,编码器的隐藏状态(通常最后的时间步)被用作解码器的开始隐藏状态,进而依次生成输出序列。通常,模型采用各种attention的变体,该注意力机制使模型根据解码器状态(通常使用softmax激活函数)有选择地关注于输入时间步中的子集。
生成输出序列的最直接方法是使用贪婪算法。不断选择每一步生成概率最大的词。但是这样通常会导致输出序列欠佳。
解决上述问题的一种常用方法是使用beam search(束搜索)。它使用广度优先搜索来构建搜索树,但在每一步只保留前N个节点,然后,将从这N个节点扩展到下一层。本质上来说,它仍然是一种贪婪算法,但由于其搜索空间较大,因此贪婪程度比真正的贪婪算法要小得多。
每个节点下面的数字是到目前为止该序列的对数概率。序列$a_1$、$a_2$、$a_3$的概率可以计算条件概率$P(a_1,a_2,a_3)=P(a_1)P(a_2 \mid a_1)P(a_3\mid a_1,a_2)$,取自然对数,可以累加。当句子结尾/序列结尾(EOS)作为最可能的预测出现时,搜索结束,并且生成了完整的序列。
高效实现Beam Search
在第一次使用N个节点启动搜索后,最朴素的方法是将这些节点作为解码器输入,运行$N$次模型。如果输出序列的最大长度为$T$,则在最坏情况下,我们必须允许模型$N \times T$。
高效的方法是将$N$个节点以批处理的方式送入到模型中。因为我们可以并行计算,所以速度会更快,尤其是在使用CUDA后端时。我们很快就会发现,更好的方法是同时进行多次束搜索。如果我们尝试为$M$个输入序列生成输出序列,则有效地批处理大小变为$N \times M$。
OpenNMT-py 实现
在translate.py里有预测/推理的代码,包含
translator = build_translator(opt, report_score=True) translator.translate(src_path=opt.src,
tgt_path=opt.tgt,
src_dir=opt.src_dir,
batch_size=opt.batch_size,
attn_debug=opt.attn_debug)
为了准确描述整个beam search过程,我们假设batch size 为3,每个样本长度为4(已经被补全过),这三个输入分别被定义为$a,b,c$:
| a1 | a2 | a3 | a4 |
| b1 | b2 | b3 | b4 |
| c1 | c2 | c3 | c4 |
_translate_batch方法将输入序列送到编码器,然后得到最后隐藏状态和每一步的输出:
src, enc_states, memory_bank, src_lengths = self._run_encoder( batch, data_type)
假定模型对每个样本/输入都有四个编码器隐藏状态,并且我们要进行大小为4的束搜索,以下代码
self.model.decoder.map_state(_repeat_beam_size_times)
扩大编码器的最后隐藏状态:
| h11 | h12 | h13 | h14 |
|---|---|---|---|
| h21 | h22 | h23 | h24 |
| h31 | h32 | h33 | h34 |
图1.编码器的最后3*4隐藏向量
变成一个$ (3 \times 4) \times 4$的向量
| h11 | h12 | h13 | h14 |
|---|---|---|---|
| h21 | h22 | h23 | h24 |
| h31 | h32 | h33 | h34 |
| h11 | h12 | h13 | h14 |
| h21 | h22 | h23 | h24 |
| h31 | h32 | h33 | h34 |
| h11 | h12 | h13 | h14 |
| h21 | h22 | h23 | h24 |
| h31 | h32 | h33 | h34 |
| h11 | h12 | h13 | h14 |
| h21 | h22 | h23 | h24 |
| h31 | h32 | h33 | h34 |
图2.扩展后的隐藏向量
它将解码器设置为一次运行$3\times4$序列(即使用批处理大小12),因此我们可以同时对这三个输入序列进行束搜索。
然后,它进入一个循环,该循环最多运行self.max_length次。在每次迭代的开始,检查停止条件后,它会通过收集最后一个时间步长的预测值来创建解码器输入(第一步输入是句子的开始符/BOS)。
# Construct batch x beam_size nxt words. # Get all the pending current beam words and arrange for forward. inp = var(torch.stack([b.get_current_state() for b in beam]) .t().contiguous().view(1, -1))
上面的声明非常重要,因此让我们仔细看看,令在前一时间步长的输入序列$(a,b,c)$的预测为$(A,B,C)$。表达式torch.stack([b.get_current_state() for b in beam],创建一个$3\times4$张量。
| A1 | A2 | A3 | A4 |
|---|---|---|---|
| B1 | B2 | B3 | B4 |
| C1 | C2 | C3 | C4 |
图3.解码器的上一次预测结果
操作.t()将张量翻转为一个$4\times3$的张量:
| A1 | B1 | C1 |
|---|---|---|
| A2 | B2 | C2 |
| A3 | B3 | C3 |
| A4 | B4 | C4 |
图4. 结果转置
.view(1,-1)将向量拉平到$1\times12$
| A1 | A2 | A3 | A4 | B1 | B2 | B3 | B4 | C1 | C2 | C3 | C4 |
图5.结果flatten
对于隐藏状态,序列以与图2中相同的模式重复。
然后将预测送入解码器:
dec_out, attn = self.model.decoder(inp, memory_bank,
memory_lengths=memory_lengths, step=i)
解码器输出被送到生成器中,以获取最终(对数)概率输出(self.model.generator.forward)。 然后将概率转换为$4\times3\times(num_words)$张量 对于每个输入序列,相应的(对数)概率输出将传递到其Beam对象(b.advance):
for j, b in enumerate(beam):
b.advance(out[:, j],
beam_attn.data[:, j, :memory_lengths[j]])
select_indices_array.append(
b.get_current_origin() * batch_size + j)
列表select_indices_array记录了Beam对象在其上展开的节点。 b.get_current_origin()返回节点的局部索引(图5中数字部分减去1)。 b.get_current_origin()\times batch_size + j恢复其在解码器输入(扩展的批处理)中的对应位置。 例如,对于第二个输入序列(j = 1),如果梁选择第二个节点进行扩展,则公式的计算公式为(2-1)* 3 +1 = 4,这指向图5中的B2。 然后将列表select_indices_array整理为一个3x4张量,翻转并最终变平,如图3-5所示。
由于可能只扩展某些节点,并且可以更改节点的顺序,因此我们需要在下一个步骤中使用select_indices_array重新对齐解码器的隐藏状态:
self.model.decoder.map_state(
lambda state, dim: state.index_select(dim, select_indices))
Beam Search 内部
两个最重要的实例变量分别是next_ys和prev_ks,可分别通过调用.get_current_state和.get_current_origin方法进行检索。 每个时间步长输出的下一个解码器的最高(beam_size)预测存储在next_ys(它们是搜索树中的节点)中。 关于上一步中的next_ys所基于的节点信息存储在prev_ks中。 它们都是从搜索树中重构输出序列所必需的。
大多数操作都在.advance方法内部完成。 它以(对数)概率输出和来自生成器的注意向量作为参数。
如果解码器不在第一时间步,则该方法将(对数)概率输出与之前的分数相加,这也是对数概率。 它代表输出序列的概率(请记住对数概率是加法的):
beam_scores = word_probs + \
self.scores.unsqueeze(1).expand_as(word_probs)
假设在我们的示例中,目标词汇量为10000,则beam_scores将为4x10000张量。 它代表40000个可能的序列及其出现的(对数)概率。
然后,该方法通过将在节点上扩展序列的概率设置为很小的值来确保它不会在EOS节点上扩展:
for i in range(self.next_ys[-1].size(0)):
if self.next_ys[-1][i] == self._eos:
beam_scores[i] = -1e20
得分/概率张量被展平,并且topk方法用于选取最可能的(beam_size)序列。 它们是要添加到搜索树中的新节点:
flat_beam_scores = beam_scores.view(-1) best_scores, best_scores_id = flat_beam_scores.topk(self.size, 0,
True, True)
该方法需要从best_score_id中恢复节点索引和令牌索引,以便分别更新prev_ks和next_ys:
# best_scores_id is flattened beam x word array, so calculate which # word and beam each score came from prev_k = best_scores_id / num_words self.prev_ks.append(prev_k) self.next_ys.append((best_scores_id - prev_k * num_words))
现在,该方法检查这些新节点,以查看它们中的任何一个是否为EOS令牌(完成输出序列)。 如果是这样,则将序列添加到列表self.finished作为输出候选:
for i in range(self.next_ys[-1].size(0)):
if self.next_ys[-1][i] == self._eos:
global_scores = self.global_scorer.score(self, self.scores)
s = global_scores[i]
self.finished.append((s, len(self.next_ys) - 1, i))
最后,它检查停止条件(如果EOS结束符号最可能位于序列的末尾)并设置eos_top标志:
# End condition is when top-of-beam is EOS and no global score. if self.next_ys[-1][0] == self._eos:
self.all_scores.append(self.scores)
self.eos_top = True
到此为止,我们覆盖整个束搜索的过程了(其中,忽略了一些细节和高级功能)。